GeoAstro
Applets
Astronomie
Chaos
Spiel
Java
Diverses
Physik
Quiz
ist es
|
|
GeoAstro Applets |
Astronomie |
Chaos Spiel |
Java |
Diverses |
Physik Quiz |
ist es |
|
Lösungen: 2. Teil (32 -
48)
1. L
33. Die Folge konvergiert (gegen P, "Papierfaltungszahl"). 34. Die Zahl P ist irrational (weder endlich noch periodisch) und sogar transzendent (nicht Lösung einer algebraischen Gleichung an xn + an-1 xn-1 + ... a1 x + a0 = 0 mit ganzen ai). 35. Mit L=0 ind R=1 erhält man 1 - P = 0.1492638117981327396... 36. P = 0, 1 1 0 1 1 0 0 1 1 1 0 0 1 0 0 1 1 1 0 1 1 0 .. Alternierendes Einfüllen von 1 und 0 in P
ergibt eine Zahl Q1: Q1 = 0, 1 1 0 1 1 0 0 1 1 1 0
0 1 0 0 1. 37. Weglassen von 1-0 ergibt eine Zahl Q2: P und Q2 sind gleich; Weglassen (Dezimieren) von 1-0 (entsprechend dem Weglassen von L- und R-Ecken) in P ändert den Wert nicht. 38. Nullen in P einfüllen ergibt eine Zahl R: R = 0, 0 1 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 1 0 1 0 0 . P ungleich R 39. Differenz von P und R: P = 0,1101100111001001...
R = 0,01010001010000010101000001.
P-R = 0,1000100010001000...
______
= 0,1000
P - R ist periodisch, also rational. 40. Dezimaler Wert von P - R= 1/2 + 2-5 + 2-9 + 2-13 + 2-17 + .... = 0,53333333... 41. P - R = s1 + s5 +s9
+s13 +s17 + ...... = s (1 + (s4)1
+ (s4)2 + (s4)3
+ (s4)4 + ......) 42. Zeige: Bei der Subtraktion in 39 steht
über einer 1 in R immer eine 1 in P (d.h. es tritt kein
Übertrag auf).
Die 1 in R an der ungeraden Position 2k+1 stand vor dem Einfüllen der Nullen auf Position k in P. Der Automat für P zeigt, daß bei einer 1 an der Stelle k auch an der Stelle 2k+1 eine 1 steht: Es sei k = a1 a2 a3 ...... an die Binärdarstellung von k; dann gilt; 2k = a1 a2 a3 ...... an 0 (d.h. der Multiplikation einer Dualzahl mit 2 entspricht das Anhängen von 0) Dann ist 2k+1 = a1 a2 a3 ...... an 1
¹ = 3.14159265358979323846 ... = [ 3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 1, 4, 1, 15, 198, ...]
47. P = 0.8507361882018672604... = [ 1, 5, 1, 2, 3, 21, 1, 4, 107, 7, 5, 2, 1, 2, 1, 1, 2, 1, 1, 1, 1, 12...] 48. Komplexe Zahlenebene In 31 wurde die Faltenfolge als reelle
Zahl P im Dualsystem (Basis 2) betrachtet: Ein geeignetes komplexes Zahlsystem
erweckt den Drachen in der Gaußschen Zahlen-ebene zum
Leben: die Darstellung ihrer Punkte durch komplexe
Zahlen der Form z = x + i y mit Real- und Imaginärteil
erfordert für ihre beiden Komponenten zwei Binärzahlen;
es genügt jedoch eine einzige Binärzahl, wenn man eine
komplexer Basis benutzt. Um sie als zweistellige
Binärzahl schreiben zu können, darf der Betrag der Basis
b nicht größer als 2 sein. Beispiele:
Die Menge aller durch Binärzahlen < 1 dargestellten komplexen Zahlen (also die Menge aller echten Brüche) bildet ein einfach zusammenhängendes Gebiet mit fraktalem Rand: den (gespiegelten) Zwillingsdrachen. Mit 2000 Punkten (2x2 Pixel) erhält man
das folgende Bild: 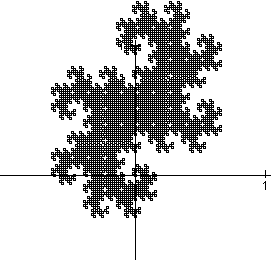
Letzte Änderung am 11. 05.
20120
|