GeoAstro
Applets
Astronomie
Chaos
Spiel
Java
Diverses
Physik
Quiz
ist es ?
|
|
GeoAstro Applets |
Astronomie |
Chaos Spiel |
Java |
Diverses |
Physik Quiz |
ist es ? |
[Aufgaben 1.Teil] [Aufgaben: 2.Teil] [Lösungen 2.Teil] ["Papierfalten]
|
1. Die Kantenlänge K wird jeweils halbiert:
Kn = K1*(1/2)n-1
(n>1) 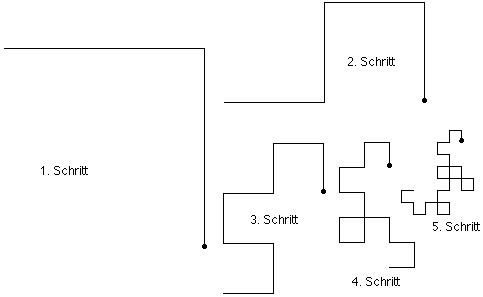 4. Die Papierdrachen werden immer kleiner. Grenzwert der Iteration ist ein Punkt. 5. 1. Schritt: L 2. Schritt: LLR 3. Schritt: LLRLLRR 4. Schritt: LLRLLRRLLLRRLRR 5. Schritt: LLRLLRRLLLRRLRRLLLRLLRRRLLRRLRR 1. Schritt (n=1): k=1 2. Schritt (n=2): k=3 3. Schritt (n=3): k=7 4. Schritt (n=4): k=15 5. Schritt (n=5): k=31 allgemein (n³1): kn+1 = 2*kn + 1 oder kn = 2n - 1 7. Beim 4. Schritt kommt erstmals eine geschlossene Masche vor, dann in allen. 8. Es treten niemals Überschneidungen auf. 9. Die mittlere Falte ist stets L; sie entspricht der ersten Faltung des Blattes nach links.
1. Bildungsgesetz ("Reflektionsgesetz") a) vorangehende Folge kopieren b) L anhängen c) jedes Symbol vor L invertieren (LÆR, RÆL) 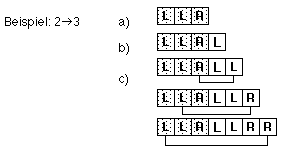
2. Bildungsgesetz: alternierendes Einfüllen von L und R 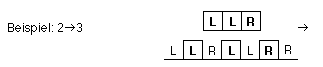
11. Es treten höchstens 3 gleiche Symbole nacheinander auf: LLL oder RRR (vgl. 8) 12. Die Folge ist nicht periodisch.
13. Das Ergebnis jeder Faltung (Output) bildet den Ausgangszustand (Input) für die folgende Faltung. 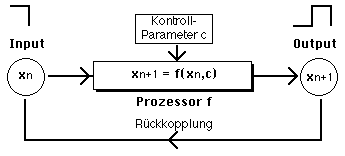 Es gibt ein geometrisches Konstruktionsverfahren, das die jeweils folgende Faltung liefert, jedoch bis auf den Maßstab (Kantenlänge) und die Orientierung. 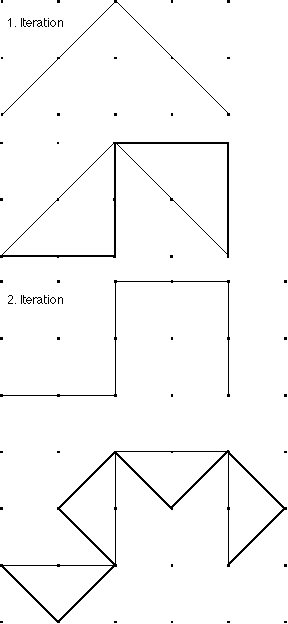
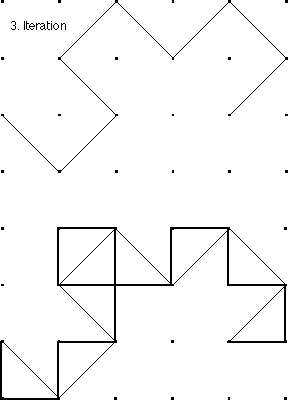 Das Konstruktionsverfahren für die nächste Iterationsstufe besteht darin, daß die Kanten durch rechtwinklige Dreiecke (mit abwechselnder Orientierung) ersetzt werden.
17. Die Gesamtgröße bleibt konstant !
Die Kantenlänge des folgenden Schritts ist:
18. Die erste Hälfte (bis zum mittleren L) ist fett gezeichnet: 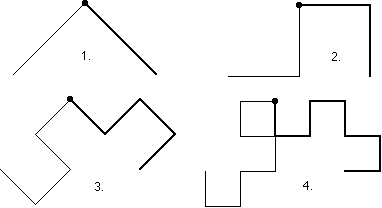
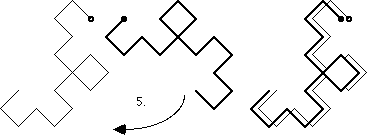
Die beiden Hälften jedes Linienzugs sind kongruent (um 90° gedreht). 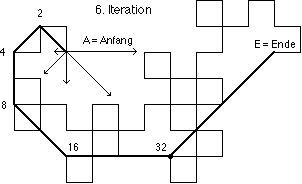
Logarithmische Spiralen besitzen ebenfalls die Eigenschaft der Selbstähnlichkeit.
21. Es entsteht eine logarithmische Spirale; in Polarkoordinaten (r,j) gilt: 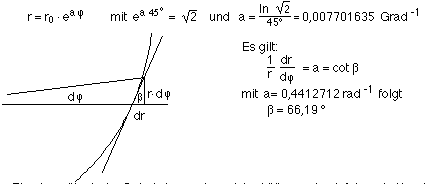 21a. Eine logarithmische Spirale besonderer Art erhält man durch folgende Konstruktion: von einem Rechteck (a>b) wird das Quadrat (b) abgeschnitten,
23. Welche "Dimension" hat die Drachenkurve ?
Die Dimension der Drachenkurve beträgt also 2, d.h. sie ist flächenfüllend ! Aneinander gelegte Drachen füllen (parkettieren) die gesamte Ebene. Zwei Drachen, der eine um 180° gedreht, lassen sich an den freien Enden zusammenfügen ("Zwillingsdrachen"): 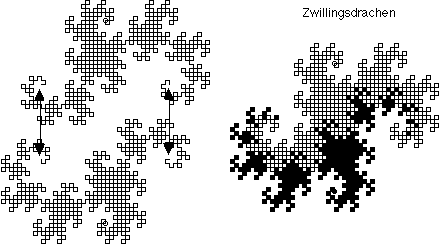
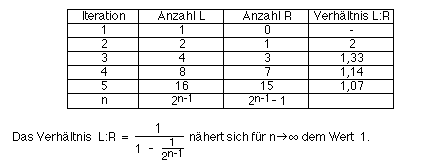 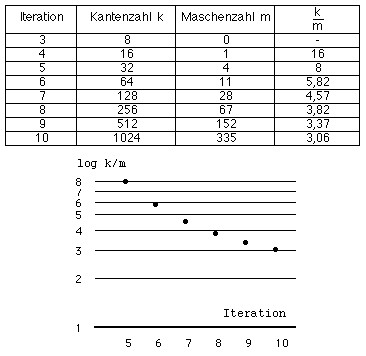
Das Verhältnis wird kleiner und scheint gegen 2 zu konvergieren.
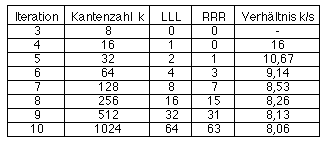
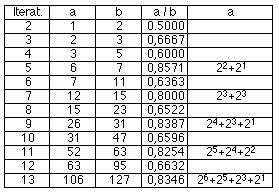
30. Mit der Kantenlänge K1 = 80
Pixel und Skalierungsfaktor 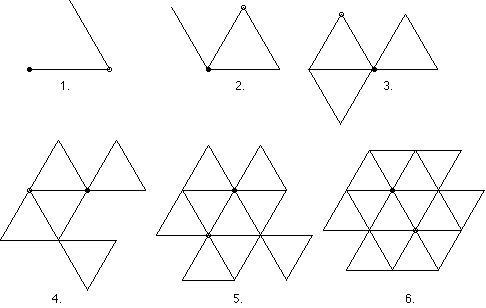
[Aufgaben 1.Teil] [Aufgaben: 2.Teil] [Lösungen 2.Teil] ["Papierfalten]
|