|
|
 GeoAstro Applets |
 Astronomie |
 Chaos Spiel |
 Java |
 Diverses |
 Physik Quiz |
 Wer ist es ? |
Papierfalten
Ein Blatt Papier und eine Schere genügen: fortgesetztes Falten erzeugt Papierschlangen, deren Gestalt zunehmend komplizierter wird. Man findet sie in Michael Crichtons Sience-Fiction Roman "DinoPark" als Ikone der "Chaostheorie":
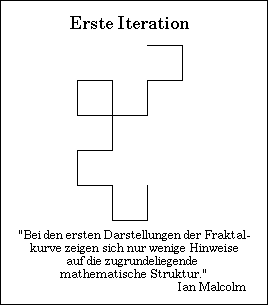
Die nacheinander ausgeführten Faltungen stellen in
mathematischer Hinsicht eine iterierte Abbildung dar. Bei passender
Skalierung liefert dieser rückgekoppelte Prozess ein Fraktal
("Drachenkurve") mit verblüffenden Eigenschaften.
Geeignete Modellbildungen erlauben genauere Untersuchungen:
unter geometrischem Aspekt zum Bildungsgesetz, zu Symmetrie, Selbstähnlichkeit, Kurvenlänge, Dimension,
und unter zahlentheoretischem Aspekt, der die Drachenkurve als Zahl auffasst. Das Papierfalten ist ein hervorragendes Beispiel für das Zusammenspiel von Experiment mit verschiedenen Teilgebieten der Mathematik.
Die Arbeitsblätter mit über 40
Aufgaben 
unterschiedlicher
Schwierigkeit eignen sich für Klassen von Unter- bis Oberstufe;
die Lösungen und Ergänzungen befinden sich im Anhang.
Die vollständige Ausarbeitung (39 Seiten) steht als Word-Dokument (für Apple Macintosh) und im pdf-Format (lesbar mit "Acrobat-Reader") zur Verfügung.
 |
Quellen:
Die Anregung zu dieser Ausarbeitung lieferte:
H.-O. Peitgen: Was hat Papierfalten mit Mathematik zu tun ? Vortrag
gehalten auf der Lehrerakademie "Chaos und Fraktale" in Bremen am
22.9.1993.
M. Crichton: DinoPark, Droemer Knaur, München 1991.
M. Schroeder: Fractals, Chaos, Power Laws, W.H. Freeman, New York
1991.
Deutsche Ausgabe:
M: Schroeder: Fraktale, Chaos und Selbstähnlichkeit, Notizen aus
dem Paradies der Unendlichkeit; Spektrum Akademischer Vlg, 1994; ISBN
3-86025-092-2.
Weitere Literatur:
B. Zühlke: Über Papierfaltfolgen und Drachenkurven zu
Methoden der Fraktalen Geometrie
MNU 50/1 (15.1.1997) Seiten 10-15
J. Carow: Aufgaben für Mathematikzirkel der Mittelstufe -
Papierfalten
MNU 50/7 (15.10.1997) Seiten 432-433
R. Albers: Drachenkurven und Selbstähnlichkeit
MNU 50/8 (1.12.1997) Seiten 456-458
Centrum für Complexe Syteme und Visualisierung (CeVis),
Universität Bremen
http://www.cevis.uni-bremen.de/education/Lehrakad.html
H.O. Peitgen, R. Albers: Papierfalten
Lehrerakademie Bremen, Materialien Band 3, Seiten 1-79 (zu beziehen
über CeVis)
Links:
Projekt Drachenkurve: http://www.tu-bs.de/schulen/stsemwob/projekte/chaos/drachen.htm
Chaos und Fraktale: http://www.fh-lueneburg.de/u1/gym03/homepage/faecher/mathe/chaos/chaos.htm
Drachenkurve als Applet: http://did.mat.uni-bayreuth.de/~alfred/Dragon/d1.html
Mathematisches Kabinett: http://did.mat.uni-bayreuth.de/mathe.html
Anleitung
|
A. Linke Kante durch Strich markieren:  |
B. Rechte Hälfte über die linke falten:  |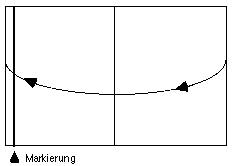
 |
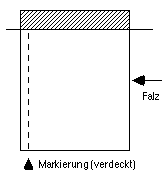D. Abgeschnittenen Streifen rechtwinklig aufklappen:  |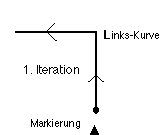
|
E. Rechte Hälfte über die linke falten:  |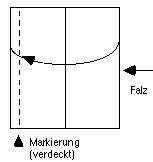
F. Streifen abschneiden:  |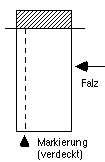
|
G. Streifen aufklappen:
|
Schritte B,C,D bzw. E,F,G wiederholen |
Die einzelnen Bilder der Iteration sind mit einem HyperCard-Stack erzeugt, der heruntergeladen werden kann (HyperCard 2.1 d).
 |
Download
"Daggon-Stack.sit.hqx" (42
kB)
|
Aufgaben 1 - 7
1. Wie ändert sich die Kantenlänge bei jedem Schritt der Faltung ?
2. Die aufgefalteten Schlangen sollen auf kariertem Papier maþstabsgetreu bis zum 5. Schritt gezeichnet werden; im 5. Schritt soll die Kantenlänge 0,5 cm betragen; mit welcher Kantenlänge muss man beginnen ?
3. Beginne jede Zeichnung mit der Falte, die der Markierung folgt, als Links-Falte:
4. Wie verhält sich die Gesamtgrösse der Papierschlangen beim weiteren Falten ?
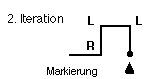
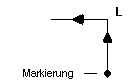
5. Notiere die Art und Reihenfolge der Falten mit den Symbolen L=Links und R= Rechts:
1. Schritt: L
2. Schritt: LLR
3. Schritt: L....................
4. Schritt: L.........................................
5. Schritt: L...................................................................................
6. Wieviel Falten gibt es nach dem 1., 2., 3., 4., ......., n-ten Schritt ?
7. Bei welchem Schritt tritt erstmals eine geschlossene Masche auf ? (Berührung zweier Kanten)
|
|
