GeoAstro
Applets
Astronomie
Chaos
Spiel
Java
Diverses
Physik
Quiz
Wer
ist es ?
|
|
GeoAstro Applets |
Astronomie |
Chaos Spiel |
Java |
Diverses |
Physik Quiz |
Wer ist es ? |
|
31. In jeder der Papierschlangen ist eine Zahl verborgen, deren Ziffern durch die Falten dargestellt werden. Für die Darstellung einer Zahl z im Stellenwert-System mit der Basis b gilt: wobei die Koeffizienten an, an-1, an-2, ...,aa1, a0 die Ziffern der Zahl z sind. Da nur zwei Arten von Falten vorkommen, ist das Dualsystem (Basis 2, Ziffern 0 und 1) besonders geeignet. Dezimal-System:
5432 = 5*1000 + 4*100 + 3*10 + 2*1
= 5*103 + 4*103 + 3*101 + 2*100
0,5432 = 5*10-1 + 4*10-2 + 3*10-3 + 2*10-4
Dual-System:
0 = 0
1 = 1
10 = 1*21 + 0*20 = 2
11 = 1*21 + 1*20 = 3
100 = 1*22 + 0*21 + 0*20 = 4
101 = 1*22 + 0*21 + 1*20 = 5
110 = 1*22 + 1*21 + 0*20 = 6
111 = 1*22 + 1*21 + 1*20 = 7
1000 = 1*23 + 0*22 + 0*21 + 0*20 = 8
1001 = 1*23 + 0*22 + 0*21 + 1*20 = 9
1010 = 1*23 + 0*22 + 1*21 + 0*20 = 10
1011 = 1*23 + 0*22 + 1*21 + 1*20 = 11
1100 = 1*23 + 1*22 + 0*21 + 0*20 = 12
1101 = 1*23 + 1*22 + 0*21 + 1*20 = 13
1110 = 1*23 + 1*22 + 1*21 + 0*20 = 14
1111 = 1*23 + 1*22 + 1*21 + 1*20 = 15
0,1 = 1*2-1 = 1*1/2 = 0,5
0,11 = 1*2-1 + 1*2-2 = 1*1/2 + 1*1/4 = 0,5 + 0.25 = 0,75
0,101 = 1*2-1 + 0*2-2 + 1.2-3 = 1*1/2 + 0*1/4 + 1*1/8 = 0,5 + 0.125 = 0,625
0,111 = 1*2-1 + 1*2-2 + 1.2-3 = 1*1/2 + 1*1/4 + 1*1/8 = 0,5 + 0.25 + 0,125 = 0,875
Wir setzen in der Faltungsfolge L=1 und R=0 und bilden
die entsprechenden Dualzahlen <1, also beginnend mit 0,...
32. Berechne die dezimalen Werte: 1. L = 0,1 = .................. 33. Welche Eigenschaft hat die Zahlenfolge ? 34. Der Grenzwert der Faltungsfolge sei P ("Papierfaltungszahl"); begründe, daß P irrational ist. 35. Welche dezimalen Werte erhält man für P, wenn L=0 und R=1 gesetzt wird ?
36. Einfüllen von 1 und 0 in P ergibt eine neue Zahl Q1:
37. Weglassen von 1-0 in P ergibt eine Zahl Q2:
Bilde Q2 und vergleiche P mit Q2. 38. Nullen in P einfüllen ergibt eine Zahl R: R = 0,0 1 0 1 0 0 0 1 1 1 . . . . . . . . . . . Vergleiche P und R. 39. Bilde die Differenz von P und R: P = 0,1101100111001001... Subtrahiere R von P. Welcher Art ist die Zahl P - R ? 40. Berechne den dezimalen Wert von P - R. 41. Zeige: P - R =s / (1 - s4) mit s = 1/2 42. Zeige: Bei der Subtraktion in 41 steht über einer 1 in R immer eine 1 in P (d.h. es tritt kein Übertrag auf).Hinweis: in R steht eine 1 stets an ungerader Position 2k+1 (k=0,1,..); benutze den Automaten für P.
43. Endlicher Automat Um das an einer bestimmten Position k stehende Symbol der Folge mit Hilfe des Bildungsgesetzes durch Reflektion zu bestimmen, sind bei großem k viele komplexe Schritte nötig; z.B. bei k=1022 sind 10 Schritte erforderlich, die Folge enthält 210=1024 Symbole. Mit einem geeigneten "endlichen Automaten" läßt sich der Aufwand erheblich reduzieren. Man stellt die Zahl k binär dar und benutzt die Ziffern dieser Darstellung als Arbeitstakte des Automaten.
44. Welche Überlegungen führen zu dem Automaten, der die Ziffern der Papierfaltungs-zahl P produziert ? 
45. Manche Irrationalzahlen besitzen trotz ihrer unendlichen Anzahl (nichtperiodischer) Stellen eine einfache Darstellung, wenn man sie als Kettenbruch schreibt. Man versteht unter einem (endlichen) Kettenbruch einen Bruch der Form 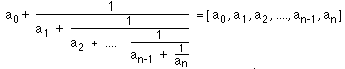
mit natürlichen Zahlen a0, a1, a2, ..., an-1, an. Man erhält die Kettenbruchentwicklung einer positiven Zahl irrationalen Zahl a , die als Dezimalzahl gegeben ist, durch folgenden Algorithmus:  Warum liefert ein Taschenrechner nur die ersten 8 bis 10 Terme der Kettenbruchentwicklung ? 46. Bestimme die Kettenbruchentwickungen für 47. Wie lautet die Kettenbruchentwickungen von P = 0.8507361882 ? 48. Die Papierfaltungs-Folge in der komplexen Zahlenebene.
|