GeoAstro
Applets
Astronomie
Chaos
Spiel
Java
Diverses
Physik
Quiz
Wer
ist es ?
|
|
GeoAstro Applets |
Astronomie |
Chaos Spiel |
Java |
Diverses |
Physik Quiz |
Wer ist es ? |
[Aufgaben: 2.Teil] [Lösungen 1.Teil] [Lösungen 2.Teil] ["Papierfalten"]
|
1. Wie ändert sich die
Kantenlänge bei jedem Schritt der Faltung ? 2. Die aufgefalteten Schlangen sollen auf
kariertem Papier maßstabsgetreu bis zum 5. Schritt
gezeichnet werden; im 5. Schritt soll die
Kantenlänge 0,5 cm betragen; mit welcher
Kantenlänge muß man beginnen ? 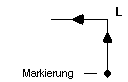 4. Wie verhält sich die Gesamtgröße der Papierschlangen beim weiteren Falten ? 5. Notiere die Art und Reihenfolge der Falten mit den Symbolen L=Links und R= Rechts:
6. Wieviel Falten gibt es nach dem 1. Schritt ? ................. 7. Bei welchem Schritt tritt erstmals eine geschlossene Masche auf ? (Berührung von Kanten) 8. Gibt es Überschneidungen ? 9. Welcher Art ist jeweils die mittlere Falte ? 10. Wie erhält man die Falten-Folge des
nächsten Schritts aus der des vorherigen ? Wie
lautet also das Bildungsgesetz ? Es gibt (2)
verschiedene Möglichkeiten der Formulierung. 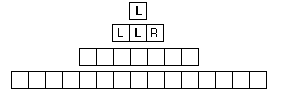 11. Wieviel gleichartige Falten treten höchstens nacheinander auf ? 12. Ist die Falten-Folge periodisch ? 13. Erläutere das Prinzip der "Rückkopplung" bei dem Prozeß des Papierfaltens. Es gibt ein geometrisches Konstruktionsverfahren, das die jeweils folgende Faltung liefert, jedoch bis auf den Maßstab (Kantenlänge) und die Orientierung. 14. Wie ergibt sich aus der 1. Faltung die 2. ? 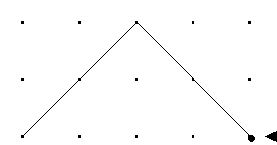 15. Wie gelangt man von der 2. Faltung zur 3. ? 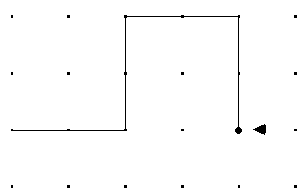 16. Und von der 3. Faltung zur 4. ? 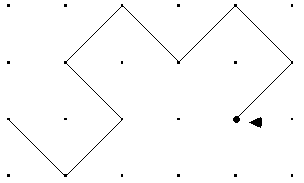 17. Wie verhält sich bei diesem Verfahren die Größe der Papierdrachen, um welchen Faktor ändert sich bei jedem Schritt die Kantenlänge ? 18. Auf Grund dieses Verfahrens läßt sich das Bildungsgesetz auf eine zweite Art angeben: 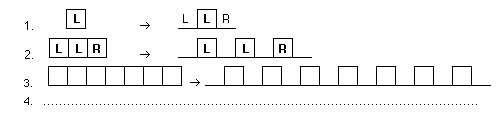 19. Zeichne die erste Hälfte jedes Drachens (von der Markierung bis zum mittleren L) in anderer Farbe nach und begründe die (für Fraktale typische) Eigenschaft der "Selbstähnlichkeit". 20. Markiere in der ersten Hälfte einer Drachenkurve (z.B. 7. Iteration) alle Mittelpunkte der vorherigen Iterationen. Was für eine Kurve entsteht dabei ?
21. Die Spirale in 20 kann durch die Gleichung r = r0 exp(a*phi) beschrieben werden 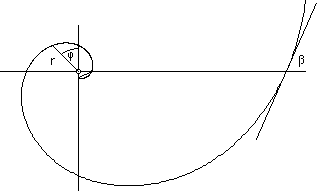 Berechne die Konstante a , wenn phi in Grad gemessen wird ? Wie groß ist der Winkel ß, unter dem jeder Radius die Tangente schneidet ? 22. Das Konstruktionsverfahren der Drachenkurve läßt sich wie folgt darstellen: der Linienzug ("Initiator", Kantenlänge K) wird durch die beiden Katheten eines rechtwinkligen Dreiecks ("Generator") ersetzt; bei der Fortsetzung ist zu beachten, daß die Orientierung der Dreiecke abwechselt.
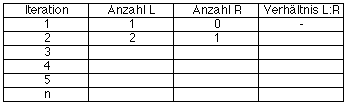 26. In der 4. Iteration tritt erstmals eine geschlossene Masche auf. Zähle in den Zeichnungen der folgenden Iterationen die Maschen und bilde das Verhältnis, in dem die Anzahl der Kanten (Geradenstücke) zur Anzahl der Maschen steht. 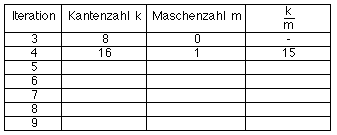 Welchem Wert sollte sich das Verhältnis nähern, wenn die Drachenkurve flächenfüllend ist ? 27. In der Zeichnung der Zeichnung des 5. Drachens kommen 4 geschlossene Maschen vor, die entsprechende Symbolfolge enthält jedoch nur insgesamt drei LLL- und RRR-Sequenzen. Erkläre. 28. Bestimme in den Symbolfolgen die Anzahl der LLL- und RRR-Sequenzen (Zählen oder aufgrund des Bildungsgesetzes): 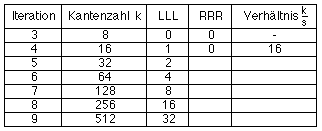
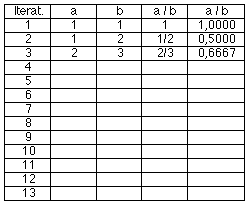 30. Beim Aufklappen der gefalteten Papierschlangen sind auch andere Winkel als 90° möglich, z.B. 60°. 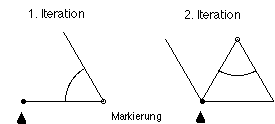
|