GeoAstro
Applets
Astronomy
Chaos Game
Java
Miscel-
laneous
Physics Quiz
Who is
Who ?
|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Physics Quiz |
Who is Who ? |
|
|
|
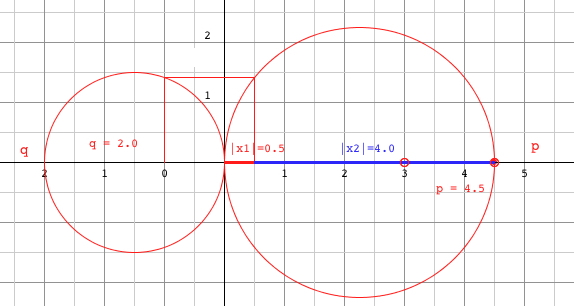
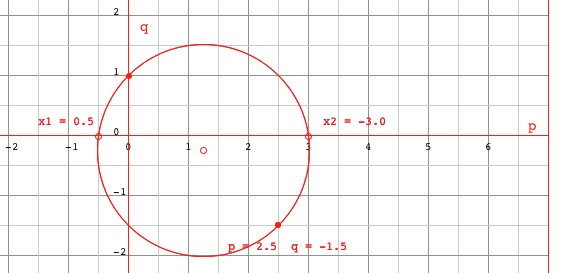
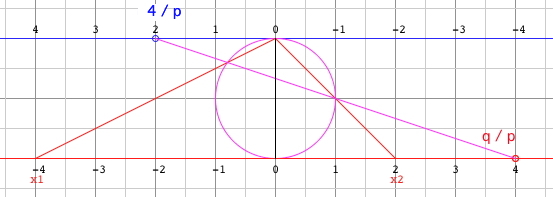
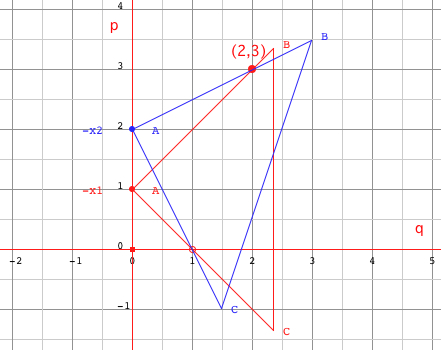
Geometric
Construction of Roots of Quadratic Equation (Cut
The Knot) Carlyle
Circle (Wolfram MathWorld) Carlyle Circle (Wolfram Demonstrations Project) Applet
showing Lill's method applied to quadratic
equations D.
Tournès: Constructions d'équation
algébriques et différentielles T.
C. Hull: Solving Cubics With Creases: The Work of
Beloch and Lill (PDF) D. W.
DeTemple: Carlyle Circles and the Lemoine
Simplicity of Polygon Constructions (PDF) Felix Klein: Famous Problems of Elementary Geometry, 1941, p. 34f (Google Books) |
R. Kaendes, R. Schmidt (Hrsg.): Mit GeoGebra mehr Mathematik verstehen, Vieweg+Teubner, 2011, ISBN 978-3-8348-1757-0. A. Baeger: Eine geometrische Lösung der quadratischen Gleichung x2 + px + q = 0, in: CASIO Forum 1/2012, CASIO Europe. E. J. Barbeau: Polynomials, Springer New York Heidelberg Berlin 2003, ISBN 0-387-40627-1, 978-0387-406275. E. John Hornsby: Geometrical and Graphical Solutions of Quadratic Equations, The College Mathematics Journal, 1990, Volume 21, Number 5, p. 362-369. Arun Kumar: A new technique of solving quadratic equations, Journal of Recreational Mathematics, Vol 14(4), 1981-82, pp 266-270. Howard Eves: An Introduction to the History of Mathematics, Saunders College Publishing, 6th ed. 1990, Chapter 3-7 (pp 87-90, 99). |
