GeoAstro
Applets
Astronomy
Chaos Game
Java
Miscel-
laneous
|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
| Karl
Georg Christian von Staudt describes a method like this
in a paper of 1841. More details can be found in a publication of Felix Klein: 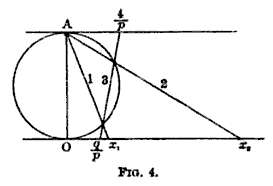 |
|
  |
The option is available
if 4/p has been fixed (upper blue axis). Checking the
box will mark certain values of q/p (lower red axis) - q is a multiple of the raster size, and - the roots x1 and x2 are multiples of the raster size. |
 |
Select the
raster size, or a continuous mode ("Raster off"). A table of p, q, x1, x2 is available by "Data Window". |
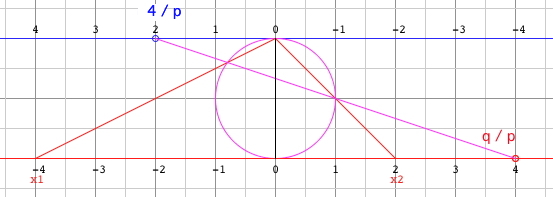 Quadratic equation: x2 + px + q = 0 Example: 4/p=2, q/p=4, equivalent p=2, q=-8, roots: x1=-4, x2=2 |
