GeoAstro
Applets
Astronomy
Chaos Game
Java
Miscel-
laneous
|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
The
only tools required by Kumar's technique are a sheet of
graph paper, and a setsquare (or a 45° right triangle).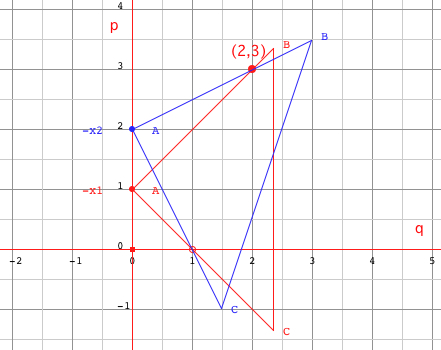 x2 + px + q = 0 - Plot the
point (q,p).
- Place the setsquare ABC: with its edge AC passing through the point (1,0) on the horizontal axis, with its apex A on the vertical axis, with the perpendicular edge AB passing through the point (q,p). - The ordinate of the point A on the vertical axis gives the negative value of one of the roots. Quadratic
equation: x2 + px + q = 0
Example:
p=3, q=2,
The proof is given in the paper of Arun Kumar.roots: x1=-1, x2=-2 |
|
 |
Checking the box will
mark certain values q, and p: - q, and p are a multiple of the raster size, and - the roots x1 and x2 (if any) are multiples of the raster size. |
 |
Select the
raster size, or a continuous mode ("Raster off"). A table of p, q, x1, x2 is available by "Data Window". |
| The curve p = 2·sqrt(q)
represents the limit between the regions of (p,q) with
reals roots existing and no real roots. It corresponds
to the discriminant D = sqrt(p2/4 - q) = 0. |
|
