|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Physics Quiz |
Who is Who ? |

Kreis falten
1.
Schneide aus einem A4-Blatt einen möglichst großen
Kreis aus (Mittelpunkt M).
2.
Markiere im Inneren des Kreises nahe dem Rand
einen beliebigen Punkt P.
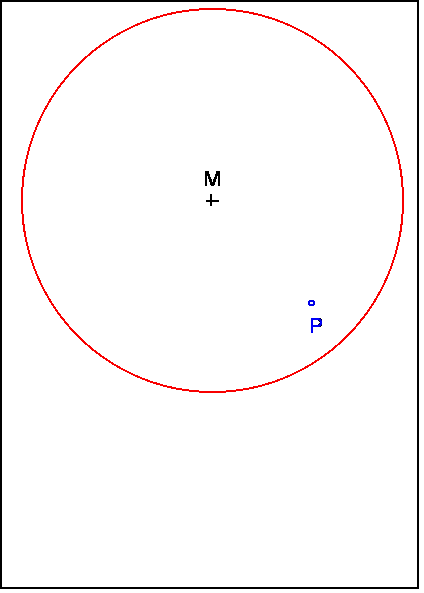
3.
Zeichne auf dem Kreisumfang einen beliebigen Punkt
Q.
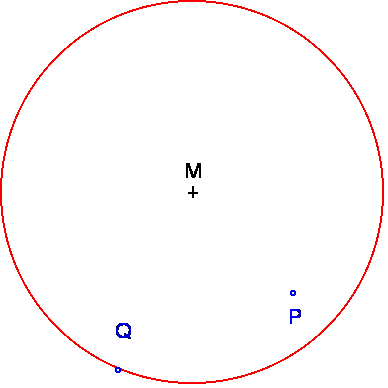
4.
Falte die Kreisscheibe so, dass der Punkt Q auf P
liegt und ziehe den Knick mit dem Daumennagel nach.
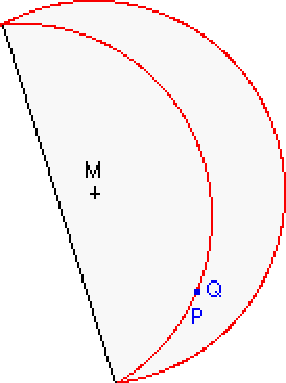
5.
Falte auf und wiederhole die Schritte 3 und 4
mehrmals mit jeweils einem anderen Punkt Q des
Kreisumfangs.
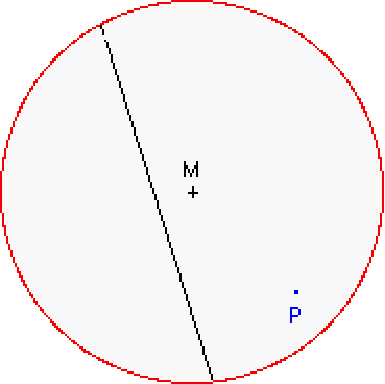
Fragen:
1. Wie sieht der Bereich aus, der keine Knicke
hat ?
2. Welche Eigenschaft hat die Gerade durch P und M
für diesen Bereich?
3. Welche geometrische Beziehung haben die
Faltgeraden für diesen Bereich?
4. Wo liegen die Punkte P und M ?
5. Welche besondere Lage haben die Punkte P und M in
dem Bereich ?
6. Konstruiere die Faltgeraden geometrisch.
Anleitung und Fragen als PDF
Anleitung
und Fragen als DOC
Hinweise zum Applet:
| - Klicke auf die
rote Kreislinie oder den Knopf "falte!" ! - Zurücksetzen und Wahl des Punktes P durch Klick in das Innere des Kreises oder Knopf "reset". - Details der Konstruktion für einzelne Faltungen können nur dann angezeigt werden, wenn P im waagerechten grauen Streifen liegt:  |
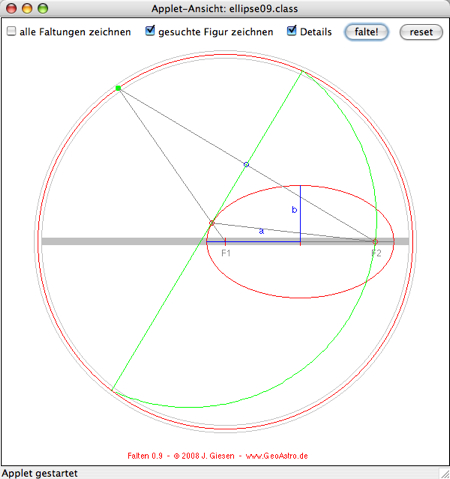
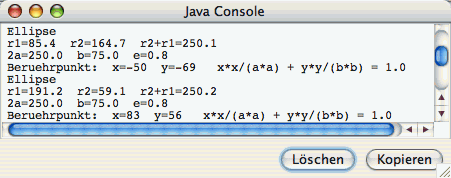
Jeder Punkt der Ellipse hat den gleichen Abstand von einem Brennpunkt und vom Leitkreis.
Zur Hyperbel
|
|
| Tangenten
an Kegelschnitte: http://members.chello.at/gut.jutta.gerhard/kegelschnitte6.htm Ellipse Leitkreis: http://haftendorn.uni-lueneburg.de/kurven/kegel/cinderella/ellipseleitkreiso.html http://haftendorn.uni-lueneburg.de/kurven/kegel/cinderella/ellipseleitkreis.html http://haftendorn.uni-lueneburg.de/kurven/kegel/leitkreis/ellipseleitkreis-ggb.html Ellipse und Leitkreis: http://members.aol.com/dustmannfw/JScatP/Ellilei1.htm Ellipse als Hüllkurve: http://members.aol.com/dustmannfw/JScatP/Ellhuell.htm Famous Curves Applet: Ellipse Equation of Ellipse Conic Enveloped by Lines Conics from Paper Folding |
(c) 2008-2023, J. Giesen
Updated: 05. Okt. 2023