|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Physics Quiz |
Folding a Circle
1.
Draw a large
circle (center
M) on a sheet of paper
and cut the circle.
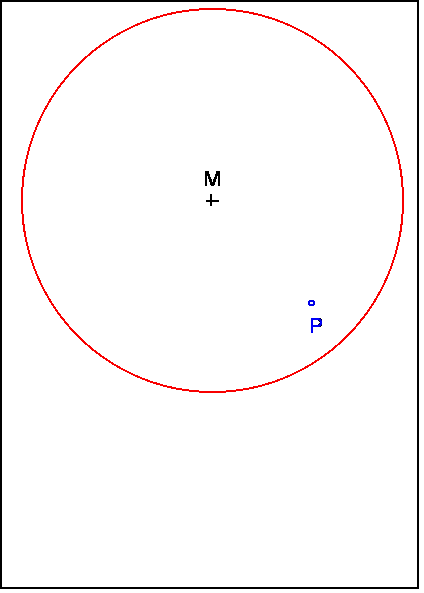
2.
Mark a point P within the circle close to the
circumference.
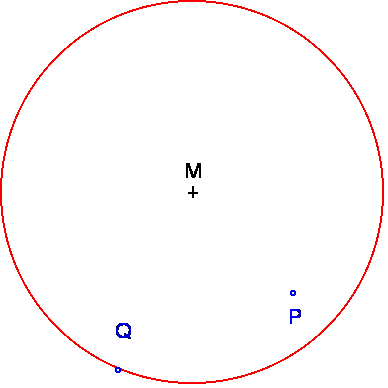
3.
Mark
a point Q on the circumference of the circle.
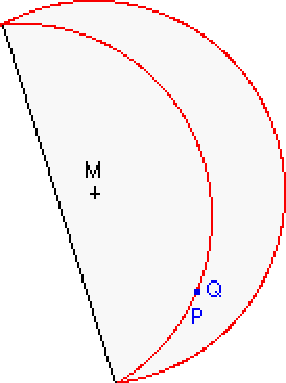
4.
Fold the paper so that the point Q on the edge of
the circle meets the point P on the interior of the
circle.
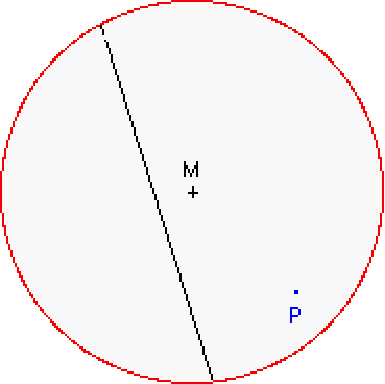
5.
Unfold the paper and repeat the steps 3 and 4 using
different points Q of the circumference.
Fragen:
1. Wie sieht der Bereich aus, der keine Knicke
hat ?
2. Welche Eigenschaft hat die Gerade durch P und M
für diesen Bereich?
3. Welche geometrische Beziehung haben die
Faltgeraden für diesen Bereich?
4. Wo liegen die Punkte P und M ?
5. Welche besondere Lage haben die Punkte P und M in
dem Bereich ?
6. Konstruiere die Faltgeraden geometrisch.
Instructions and Questions (PDF)
Instructions
and Questions (DOC)
Using the Applet:
| - Click the red
circle or press the button "fold!" ! - Reset and select the point P by clicking the interior of the circle or use the button "reset". - Details of the construction are displayed in case P is within the gray rectangle:  |
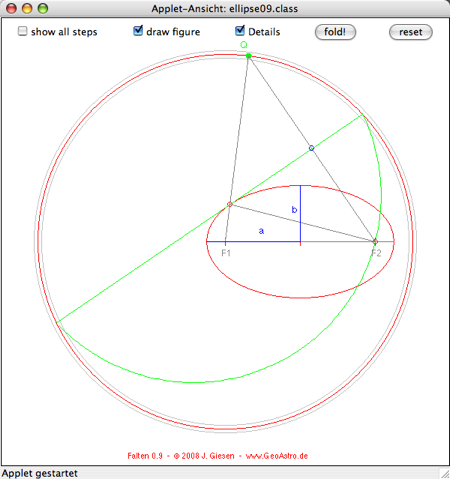
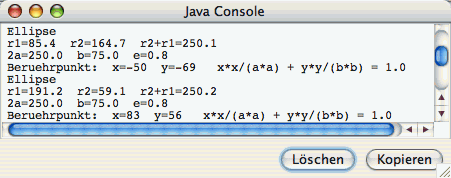
Jeder Punkt der Ellipse hat den gleichen Abstand von einem Brennpunkt und vom Leitkreis.
Hyperbola
|
|
| Tangenten
an Kegelschnitte: http://members.chello.at/gut.jutta.gerhard/kegelschnitte6.htm Ellipse Leitkreis: http://haftendorn.uni-lueneburg.de/kurven/kegel/cinderella/ellipseleitkreiso.html http://haftendorn.uni-lueneburg.de/kurven/kegel/cinderella/ellipseleitkreis.html http://haftendorn.uni-lueneburg.de/kurven/kegel/leitkreis/ellipseleitkreis-ggb.html Ellipse und Leitkreis: http://members.aol.com/dustmannfw/JScatP/Ellilei1.htm Ellipse als Hüllkurve: http://members.aol.com/dustmannfw/JScatP/Ellhuell.htm Famous Curves Applet: Ellipse Equation of Ellipse Conic Enveloped by Lines Conics from Paper Folding |
(c) 2008-2023, J. Giesen
Updated: 20.10.2023