Home Site Map Search

GeoAstro Applets

Astronomy

Chaos Game

Java

Miscel- laneous

Moonflight Applet

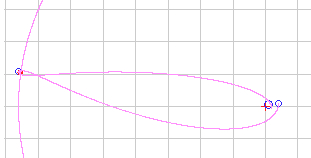
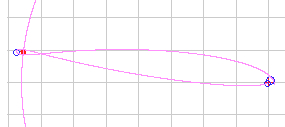
The applet computes and displays the orbit of a spacecraft sent off from the Earth's orbit to travel to the Moon. The transfer orbit is treated as a restricted three body problem. The perturbations by the Sun, and all the other bodies in the Solar system are neglected. The orbit of the Moon is supposed to be circular (eccentricity only 0.055), and the initial orbit around the Earth is in the orbital plane of the Moon. 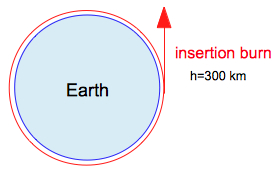Initial orbit of the spacecraft around the Earth: h=300 km above surface v=7.731 km/s The insertion burn velocity at h=300 km is preset to v0=10.85 km/s (Δ v=4.922 km/s), the position angle of the Moon to Φ0 = 120.0° After insertion burn the spacecraft is performing a free flight around the Moon and back to the Earth. 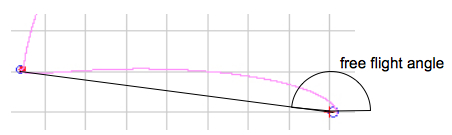The values of altitude h are 500 km,  300 km, and 150 km, v0 and Φ0 can be changed in small steps of +/- 0.005 km/s and +/- 0.25° by the very right menu: The orbit of the spacecraft is very sensitive to initial values of v0 and Φ0 ! The origin of the coordinate system (x,y) lies in the center of gravity of the Earth and the Moon, located at 4675 km from the Earth's center. The applet is using the Cauchy midpoint method, and a variable step size dt depending on the distance from the Earth and the Moon. Using the default steps dt is between 1.2 s and 120 s, taking about 28,000 steps for a complete flight returning to the Earth. dt may be decreased or increased by a menu:

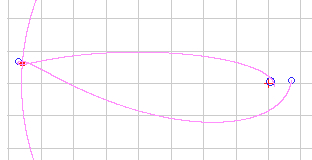
Applet features: Example 1: h=500 km, v0=10.7 km/s, Φ0 = 129.0° total flight time 153 h closest approach to the surface of the Moon: h=1315 km Another set of initial values: 500 km, 10.69 km/h, 128.75° Example 2: h=300 km, v0=10.85 km/s, Φ0 = 120.0° total flight time 183 h closest approach to the surface of the Moon: h=4875 km Another set of initial values: 300 km, 10.835 km/h, 119.75° Example 3: h=150 km, v0=10.985 km/s, Φ0 = 126.0° total flight time 189 h closest approach to the surface of the Moon: h=8467 km crash on return to Earth Another set of initial values: 150 km, 10.98 km/h, 126.0° To explore the far (invisible) side side of the Moon the launch should take place about 88 hours before New Moon. The passage of the far side lasts about 20 minutes (the relative velocity of Moon and spacecraft is about 1.6 km/s). Select "Diagram r(t), v/t)": 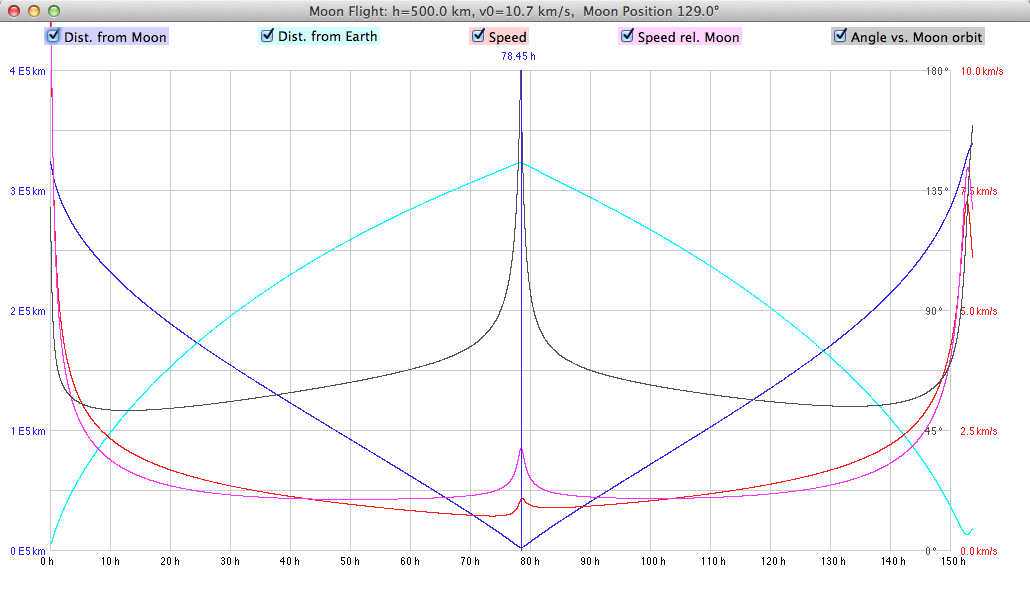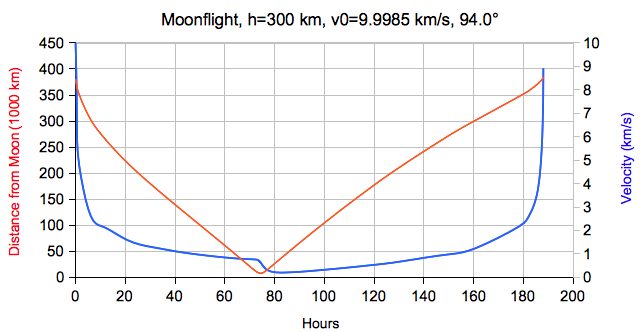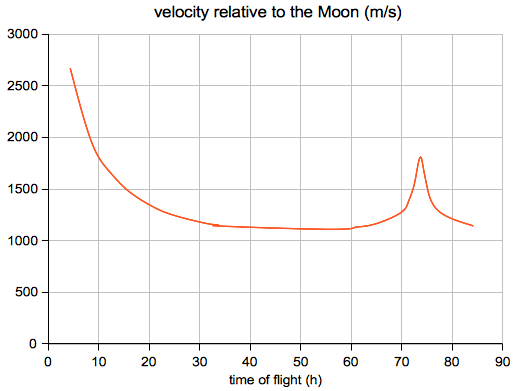Neglecting the attraction by the Moon we get the following time of flight for ellipses intersecting the Moon's orbit as a function of the injection speed v0 (injection orbit h=300 km): The maximum value is v0 = sqrt(2*G*mEarth/r0) 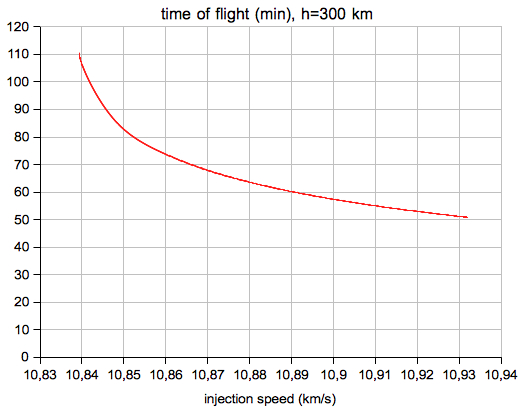Select "Diagram  r(t), v(t)" from the very right menu: In a restricted three body problem the total energy W and the angular momentum L are not preserved: 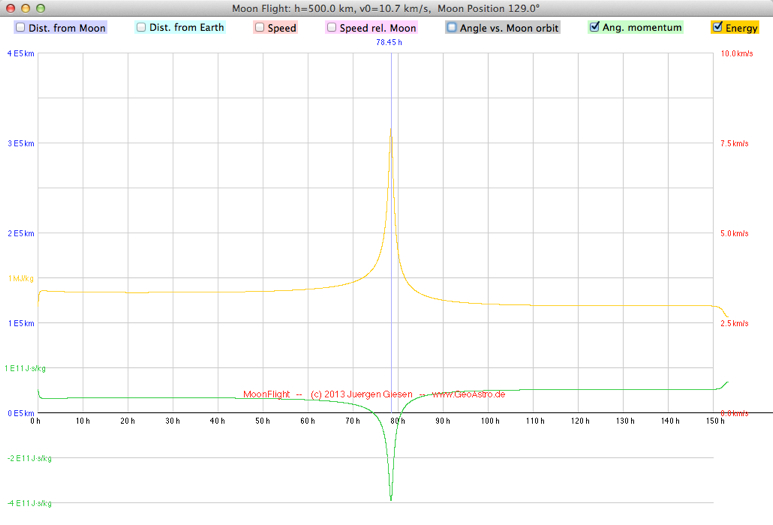After the probe has passed the Moon select "Arrival orbit" from the very right menu: 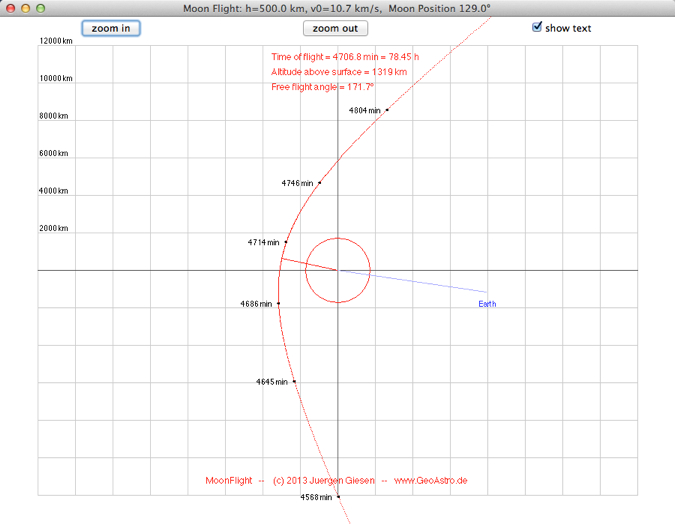Note that this view is relative to the moving Moon, which is different from the view relative to the center of mass.

Web Links

Hohmann transfer orbit (Wikipedia) Fundamentals of Orbital Mechanics Hohmann Transfer Flight to Mars: How Long? Along what Path? Walter Hohmann (Wikipedia) Walter Hohmann: The Attainability of Heavenly Bodies (PDF) Walter Hohmann’s Roads In Space (William I. McLaughlin) Lecture L17 - Orbit Transfers and Interplanetary Trajectories Apollo 11 (Wikipedia)

Books

Konstantin Ziolkowski: Die Erforschung des Weltraums mit Rückstoßgeräten; 1903. Walter Hohmann. Die Erreichbarkeit der Himmelskörper, 3. Auflage, Oldenbourg, München und Wien 1994, ISBN 978-3486231069 Hermann Oberth: Die Rakete zu den Planetenräumen, 1923. Nachdruck: Michaels-Verlag, 1984, ISBN 3-89539-700-8 Hermann Oberth: Wege zur Raumschiffahrt, Dritte, stark erweiterte Auflage von "Die Rakete zu den Planetenräumen",  1929. Nachdruck VDI Verlag 1986, ISBN 3-18-400755-3 Willy Ley (Hrsg.): Die Möglichkeit der Weltraumfahrt, Hachmeister & Thal, Leipzig 1928. Rudolf Nebel: Raketenflug, 1932. Max Valier: Der Vorstoß in den Weltraum, Oldenbourg, München und Berlin, 1. Auflage 1924. Max Valier: Raketenfahrt, Oldenbourg, München und Berlin, 5. Auflage 1928 Otto Willy Gail: Physik der Weltraunfahrt; Reich Verlag, München 1948.   Willy Ley: Vorstoss ins Weltall, Rakete und Raumschiffahrt; Universum Verlagsgesellschaft, Wien 1949. Paul Hellings: Astrophysics with a PC, An Introduction To Computational Astrophysics; Willmann-Bell, Richmond Verginia 1994. Roger R. Bate, Donald D. Mueller Jerry E. White: Fundamentals of Astrodynamics, Dover Publications, New York 1971.

Science Fiction

Jules Verne: De la Terre à la Lune, Trajet direct en 97 heures 20 minutes; 1865 Jules Verne: De la Terre à la Lune, Trajet direct en 97 heures 20 minutes; 1865 (PDF) Otto Willy Gail: Der Schuß ins All, Ein Roman von morgen; Breslau 1925 Otto Willy Gail: Der Stein vom Mond, Kosmischer Roman; Breslau 1926

© 2013-2023 J. Giesen

Modified 2023, Oct 14