|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Hohmann Transfer Orbit Applet
|
The applet computes and displays the orbit
of a spacecraft
sent off from the Earth's orbit to travel to an
inner or outer planet of the solar system. The transfer orbit is treated as
a simple Keplerian ellipse around the Sun. The
perturbations by the Earth, the target planet, and
all the other bodies in the Solar system are
neglected. The orbits of the Earth and the target
are both supposed to be circular, inclination of the orbit against
the plane of the Earth is neglected.
In 1925 Walter Hohmann
(1880-1945) recognized that the minimum energy
orbit between two circular orbits is an ellipse
which is tangent at the perihelion of one orbit
and at the aphelion of the other. |
|
The launch is in the direction of the of the
origin planet's orbit to take advantage of its
kinetic energy. To reach an outer
planet: To reach an inner
planet:
|
| from Earth | to Sun | to Mercury | to Venus | to Mars | to Jupiter | to Saturn | |
| orbital radius | 1 AU |
0.0050 AU | 0.3871 AU | 0.723 AU | 1.524 AU | 5.204 AU | 9.582 AU |
| orbital period | 365.24 d |
0.1 d | 88.0 d | 224.7 d | 687.0 d | 4332.6 d | 10833.9 d |
| orbital velocity | 29.79
km/s |
436.6 km/s | 47.88 km/s | 35.03 km/s | 24.13 km/s | 13.06 km/s | 9.62 km/s |
| launch
velocity |
2.87 km/s | 22.25 km/s | 27.32 km/s | 32.74 km/s | 38.58 km/s | 40.09 km/s | |
| launch burn | -26.92 km/s | -7.53 km/s | -2.47 km/s | 2.95 km/s | 8.79 km/s | 10.30 km/s | |
| transfer orbit s-m axis |
0.502 AU | 0.694 AU |
0.862 AU | 1.262 AU | 3.102 AU | 5.291 AU | |
| transfer
orbit eccentricity |
0.991 | 0.442 | 0.160 | 0.208 | 0.678 | 0.811 | |
| transfer
orbit path length |
1.03 AU | 2.07 AU |
2.69 AU | 3.92 AU | 8.51 AU | 13.40 AU | |
| transfer
time |
65.0 d | 105.5 d |
146.1 d | 258.9 d | 997.8 d | 2222.7 d | |
| arrival velocity | 616.0 km/s | 57.49 km/s | 37.73 km/s | 21.48 km/s | 7.41 km/s | 4.18 km/s | |
| arrival burn | -179.4 km/s | -9.61 km/s | -2.71km/s | 2.65 km/s | 5.64 km/s | 5.44 km/s |
Earth - Moon Transfer Orbit:
| Flight
Time |
|
| Hohmann | 119.5 h |
| Jules
Verne, Science
Fiction |
97.3 h |
| Apollo 11, after Trans Lunar Injection
Burn |
72.0 h |
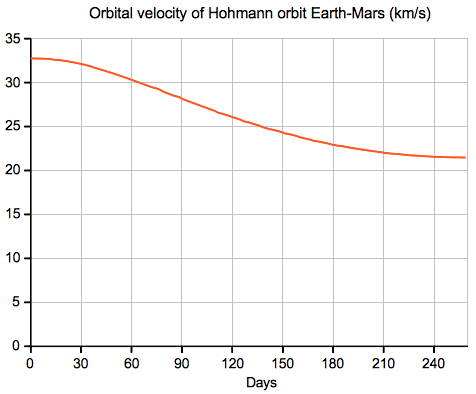
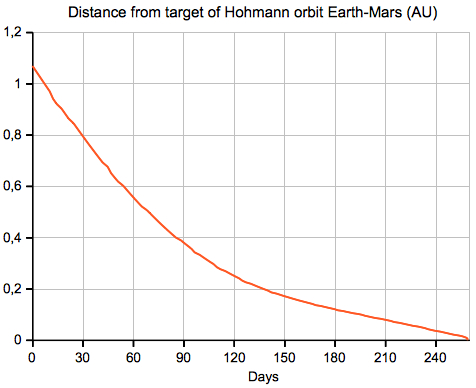
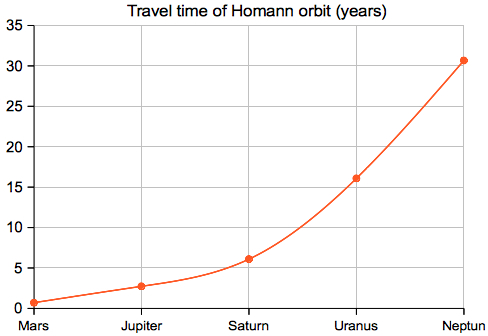
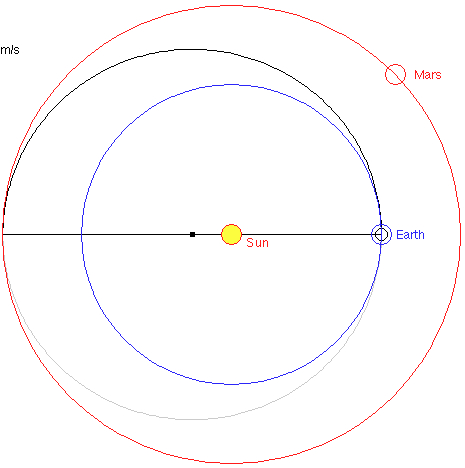
Details for Earth-Mars Transfer and Return:
The "Target Mars" option only is including the return flight from Mars to Earth
 |
 |
| Start
from Earth, t=0 Mars is 44.3° ahead |
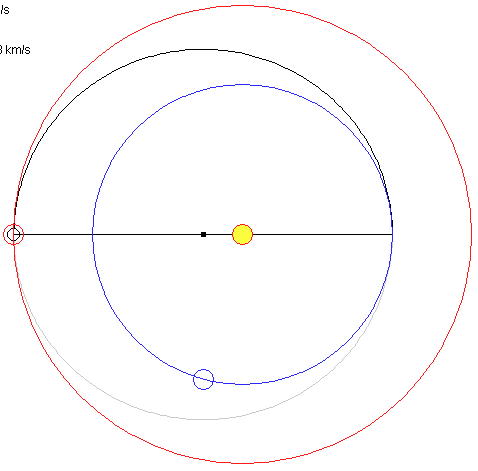
Arrival
at Mars, t = 258.9 days Earth is at 255.2° |
 |
 |
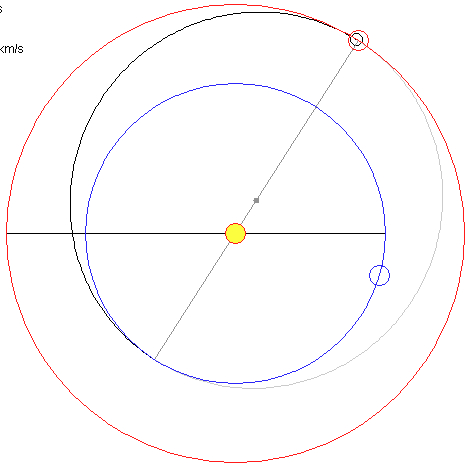
Waiting for 454.1 days, t = 713.1 days Earth is at 342.8° |
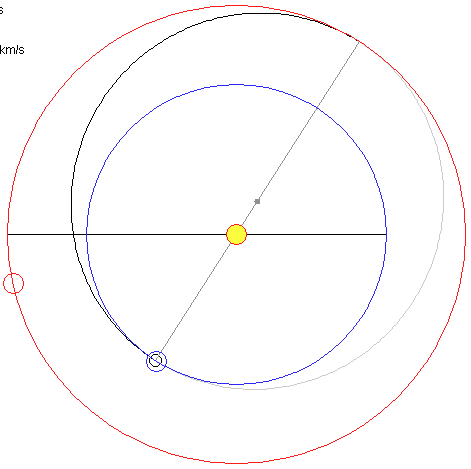
Arrival on Earth, t = 970.8 days |




|
|
|
Hohmann transfer
orbit (Wikipedia) Fundamentals of Orbital Mechanics Flight to Mars: How Long? Along what
Path? Walter
Hohmann: The Attainability of Heavenly Bodies
(PDF) Walter Hohmann’s Roads In Space
(William I. McLaughlin) Lecture L17 - Orbit Transfers and
Interplanetary Trajectories |
| Books |
| Konstantin Ziolkowski: Die
Erforschung des Weltraums mit Rückstoßgeräten; 1903. Walter Hohmann. Die Erreichbarkeit der Himmelskörper, 3. Auflage, Oldenbourg, München und Wien 1994, ISBN 978-3486231069 Hermann Oberth: Die Rakete zu den Planetenräumen, 1923. Nachdruck: Michaels-Verlag, 1984, ISBN 3-89539-700-8 Hermann Oberth: Wege zur Raumschiffahrt, Dritte, stark erweiterte Auflage von "Die Rakete zu den Planetenräumen", 1929. Nachdruck VDI Verlag 1986, ISBN 3-18-400755-3 Willy Ley (Hrsg.): Die Möglichkeit der Weltraumfahrt, Hachmeister & Thal, Leipzig 1928. Rudolf Nebel: Raketenflug, 1932. Max Valier: Raketenfahrt, Oldenbourg, München und Berlin, 5. Auflage 1928 Otto Willy Gail: Physik der Weltraunfahrt; Reich Verlag, München 1948. Willy Ley: Vorstoss ins Weltall, Rakete und Raumschiffahrt; Universum Verlagsgesellschaft, Wien 1949. |
| Science Fiction |
| Jules Verne: De la Terre à la
Lune, Trajet direct en 97 heures 20 minutes; 1865 Jules Verne: De la Terre à la Lune, Trajet direct en 97 heures 20 minutes; 1865 (PDF) Otto Willy Gail: Der Schuß ins All, Ein Roman von morgen; Breslau 1925 Otto Willy Gail: Der Stein vom Mond, Kosmischer Roman; Breslau 1926 |
©
2013-2023 J. Giesen
Modified:
2023, Oct 04