|
|
GeoAstro Applets |
Astronomie |
Chaos Spiel |
Java |
Diverses |
Physik Quiz |
Wer ist es ? |
|
"Un
astre lumineux, de la même densité que la Terre, et
dont le diamètre serait 250 fois plus grand que le Soleil, ne
permettrait, en vertu de son attraction, à aucun de ses rayons
de parvenir jusqu'à nous. Il est dès lors possible que
les plus grands corps lumineux de l'univers puissent, par cette cause,
être invisibles".
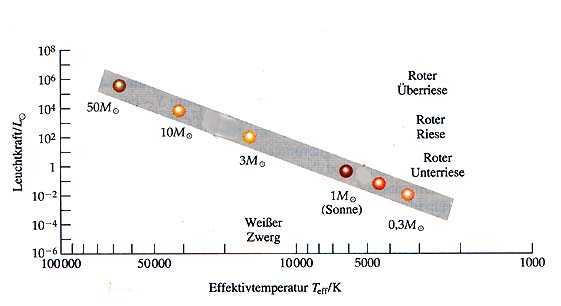
Weiße Zwergsterne haben trotz verhältnismäßig hoher Temperatur nur eine geringe Leuchtkraft und müssen daher sehr klein sein. Ihre mittlere Dichte liegt in der Größenordnung 108 kg/m3 bis 109 kg/m3 (Sonne: 1,4·103 kg/m3). Die Gravitation komprimiert den Atomradius auf ein Hundertstel seines üblichen Wertes. Der Druck der Elekronen kann dem Gravitationsdruck standhalten und der Stern ist stabil, sofern seine Masse des Sterns unter etwa 1,4 Sonnenmassen bleibt (Chandrasekhar-Grenze). Der Radius eines Weißen Zwergs beträgt etwa 10.000 km (Sonne: 693.000 km). Beim Zusammenbruch von massereichen Sternen (2 bis 10 Sonnenmassen) steigt die Energie der Elektronen solange, bis aus Elektron und Proton ein Neutron entsteht: Der Gravitationskollaps schreitet bis zu einer Dichte von etwa 1017 kg/m3 fort. Dies entspricht der Dichte von Atomkernen. Der Stern besteht dann aus dicht gepackten Neutronen, deren Druck den Zusammenfall zum Stillstand bringt (Neutronenstern). Der Radius eines Neutronensterns beträgt etwa 10 km. Kollabiert ein Stern mit einer Masse von mehr als 10 Sonnenmassen (M>10 MS) tritt eine Besonderheit auf. 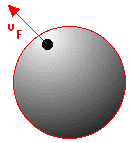 Unterschreitet der Radius des Sterns den von Schwarzschild angegebenen Gravitations-Radius ("Schwarzschild-Radius") wird die Gravitationskraft so stark, dass weder Licht noch Teilchen die Sternoberfläche verlassen können: der Stern wird zu einem Schwarzen Loch. Ein Schwarzes Loch mit der Masse von 10 Sonnen hat den Schwarzschild-Radius R = 29 km. Der obige Radius RS (herzuleiten aus der von Schwarzschild angenommenen Metrik des Raumes in einem Gravitationsfeld) ergibt sich (bis auf den Faktor 2) auch aus einer einfachen Energiebilanz für die Flucht eines Photons (Masse m) aus dem Gravitationsfeld:
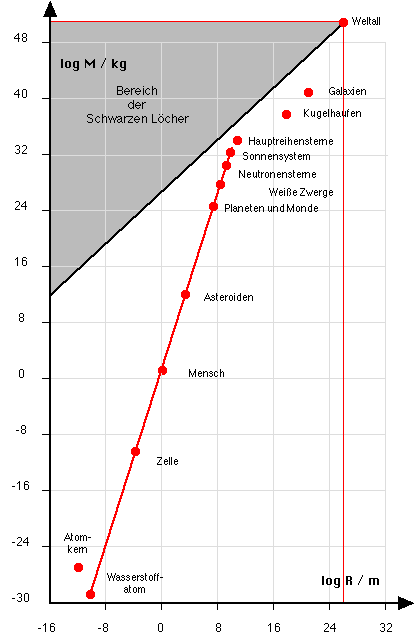
Das Diagramm zeigt in logarithmischer Darstellung den Zusammenhang zwischen der Masse M und der Ausdehnung R für verschiedene Objekte des Universums.
Wie lange dauert der Kollaps eines Sterns mit 10 Sonnenmassen und Sonnenradius auf RÅ0 ? Bei konstanter Beschleunigung g folgt aus t = [2 R3 / (GM)]1/2 = 72 s Der Kollaps zu einem Neutronenstern oder zu einem Schwarzen Loch erfolgt also in wenigen Sekunden.
Letzte Änderung: 4.4.2007 |