Home Site Map Search

GeoAstro Applets

Astronomy

Chaos Game

Java

Miscel- laneous

Physics Quiz

Who is Who ?

back to Astrophysics   The Roche Limit The Roche limit is the minimum orbital radius which is necessary for dust or particles to grow forming a moon, or necessary for an existing moon to remain internally stable. It is named after Édouard Roche (1820 – 1883).   Determining the Roche limit Two particles (mass m, radius r) orbiting the planet (mass M) will be bound, if their mutual gravitational force F = G*m*m/(2r)2 is greater than the difference of the gravitational forces ((tidal force) exerted by the body of mass M  on the particles at R-r and R+r ΔF = F2 - F1 = G*m*M/(R-r)2 - G*m*M/(R+r)2 ΔF = (G*m*M/R2)*[1/(1-r/R)2 - 1/(1+r/R)2] For m<<M (or r/R<<1): 1/(1-r/R)2 - 1/(1+r/R)2 ≈ 1/(1-2r/R) - 1/(1+2r/R) ≈ 1+2r/R - (1-2r/R) = 4r/R The Roche limit is given by the condition: ΔF = F (G*m*M/R2)*4r/R = G*m*m/(4r2) M*4r/R3 = m/(4r2) R = r*(16*M/m)1/3 ≈ 2.5*r*(M/m)1/3 Using the densities of the bodies m=ρm*4π*r3/3 and M=ρM*4π*rM3/3: R = r*(16*M/m)1/3 = rM*(16*ρM/ρm)1/3 In case of equal densities, ρM = ρm R ≈ 2.5*rM radius density  Roche limit R orbit radius Earth 6.378 km 5,510 kg/m3 18,970 km 384,400 km = 1/20 R Moon 3,350 kg/m3 radius density  Roche limit R orbit radius Sun 696,000 km 1,410 kg/m3 1,113,000 km 149,600,000 km = 1/134 R Earth 5,510 kg/m3 In the solar system the orbits of the Earth's moon and of the Earth are in a region of stability. The Hill Sphere An astronomical body's Hill sphere is the region in which it dominates the attraction of satellites. It is named after John William Hill (1812–1879). 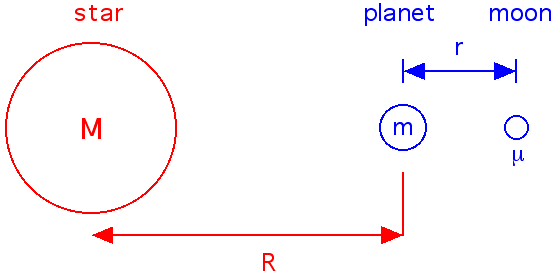Determining the Hill Sphere radius The satellite or moon (mass μ) is orbiting the star (mass M) with the same angular velocity ω at the distance R+r as the planet (mass m) at the distance R (permanent full moon position). The equilibrum condition for the planet is: m ω2 R = G m M/R2 ω2 = GM/R3 The satellite is dragged by the combined gravitational forces exerted by the star and the planet: μ ω2 (R+r) = G μ M/(R+r)2 + G μ m/r2 Inserting ω2: G μ M (R+r)/R3 = G μ M/(R+r)2 + G μ m/r2 M (R+r)/R3 = M/(R+r)2 + G m/r2 M (R+r)3 r2 = M R3 r2 +  m R3 (R+r)2 m R3 (R+r)2 = M r2 (R3+3R2r+3Rr2+r3) - M R3 r2 m R3 (R+r)2 = M r3 (3R2+3Rr+r2) For r<<R: (R+r)2 ≈ R2, and 3Rr+r2 ≈ 0. The equation simplifies: m R5 = 3 M r3 R2 m R3 =  3 M r3 r = R [m/(3M)]1/3 mass orbit radius Hill sphere r orbit radius moon Sun 1.99×1030 kg 149,600,000 km 1,496,000 km 384,400 km = 1/4 r Earth 5.97×1024 kg Web Links Roche limit (Wikipedia) Hill sphere (Wikipedia)   Last update 2015, Jun 18