Home Site Map Search

GeoAstro Applets

Astronomy

Chaos Game

Java

Miscel- laneous

Sun & Moon Polar Applet

	Select latitude (northern positive, southern negative), and longitude (eastern negative, western positive) from the menus.
	You may use the keys "y", "m", "d", "h", "n" to increase the year, month, date, hour, or minute, or Shift key and "y", "m", "d", "h", "n" to decrease the year, month, date, hour, or minute.

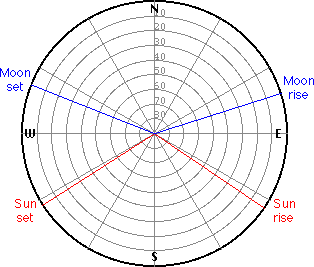
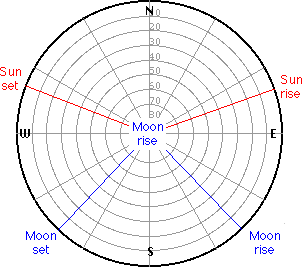
How to get the applet version for offline use Berlin, 2003, April 16 at 20:26 CEST   Applet: Sun and Moon azimuth at Horizon showing a diagram for one year Watch the points (azimuth angles) of rise and set of the Sun and the Moon on the horizon as the are changing from day to day: Berlin, 2003 Jan 21 Berlin, 2003 Apr 21 Watch animation The azimuth angle Az0 for rise and set can be computed from the declination (delta) and the geographical latitude (beta) by: cos (Azo) = sin delta / cos beta At Berlin (beta=52.51°) we get for the: rising Sun declination Azimuth Az0 23.44° summer solstice 49.2° -23.44° winter solstice 130.8° 0° equinox 90° rising Moon (orbit inclination to ecliptic 5.145°) declination Azimuth Az0 +23.44° + 5.145° = = 28.585° 38.2° +23.44° - 5.145° = 18.295° 58.95° -23.44° + 5.145° = -18.295° 121.05° -23.44° - 5.145° = -28.585° 141.8° 0° + 5.145° = 5.145° 81.5° 0° - 5.145° = - 5.145° 98.5° 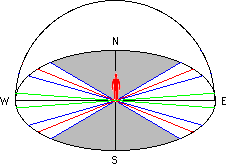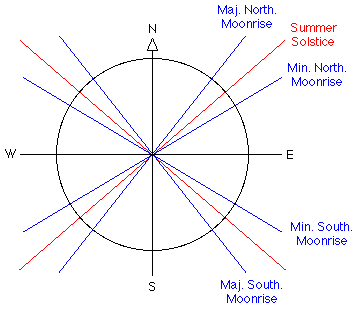Moonrise and moonset may occur at any point of the horizon except in the grey sector:   Whereas the range of the azimuth angle of rise and set is constant for the sun, it varies for the moon: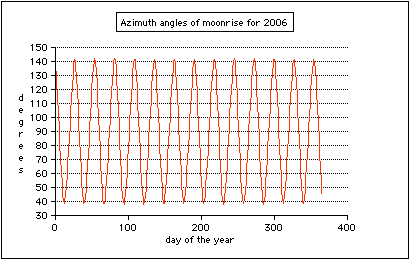

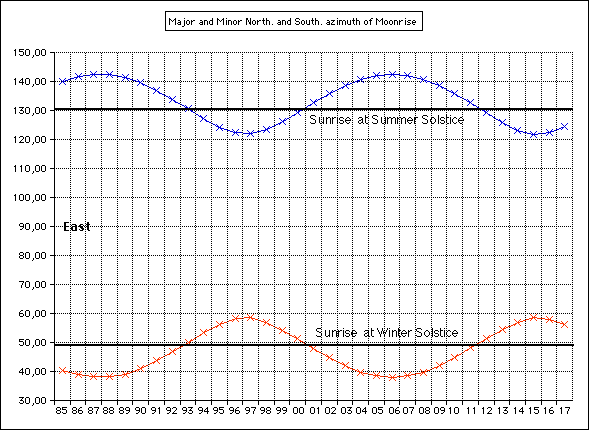
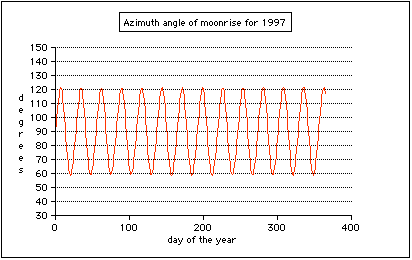
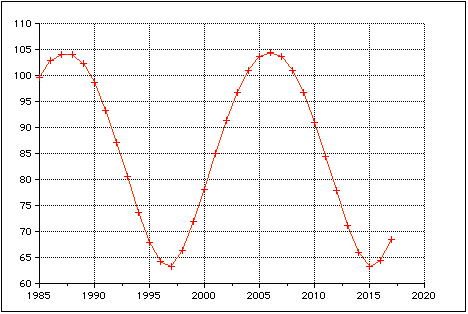
Berlin, 1985 - 2017,
Major and minor northern and southern moonrise azimuth

In this diagram we find a period of about 18.5 years, the time for a turn of the line of nodes which rotates in the opposite direction to the Moon's movement ("regression of the nodes"). 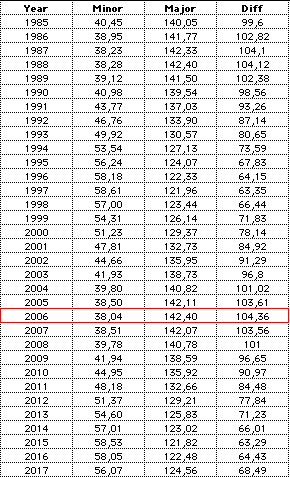2006 is a major lunar standstill season. Angular difference between major and minor moonrise azimuth     Solstice Azimuth Applet  The directions of solar and lunar standstill are found at the Stonehenge observatory Latitude beta = 51.18 N, Obliquity delta=24.0° (3000 BC). green: moon azimuth for declination -5.145° and +5.145° blue: moon azimuth for declination 24.0°-5.145° and 24.0°+5.145°, -24.0°-5.145° and -24.0°+5.145°, red: moon azimuth for declination 24.0° and -24.0°, Sun at solstices. The applet is using the simple azimuth formula cos(Azo) = sin(delta)/cos(beta) describing a "mathematical" sunrise (center of the Sun on the horizon, no atmospheric refraction). Using the common definition of sunrise (elevation -0.83°), the azimuth angle of the rising Sun is about 1.3° smaller at summer solstice. 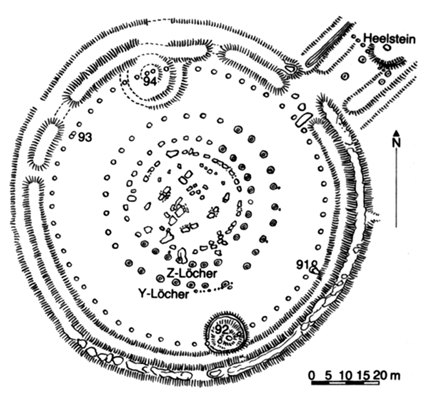"Grundriss von Stonehenge. Von aussen nach innen: Graben, Wall, Aubrey-Löcher, Stationssteine 91-94, Y- und Z-Löcher, Sarsenkreis, Hufeisen, einige Blausteinpfeiler und, verstreut, Pfostenlöcher." Quelle: Rudolf Drößler: Astronomie in Stein. Archäologen und Astronomen enträtseln alte Bauwerke und Kultstätten. Lizenzausgabe Panorama Verlag, Wiesbaden, o.J., ISBN 3-926642-25-4. Seite 71, Bild 33. 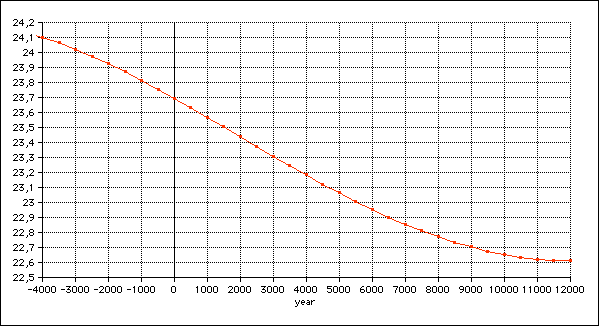Die Wiedergabe erfolgt mit freundlicher Genehmigung des Verfassers. Obliquity of the ecliptic:    rising Sun declination Azimuth Az0 24.0° summer solstice 49.5° -23.44° winter solstice 130.5 rising Moon (orbit inclination to ecliptic 5.145°) declination Azimuth Az0 +24.0° + 5.1° = 29.1° 39.1° Maj. Northern +24.0° - 5.1° = 18.9° 58.9° Min. Northern -24.0° + 5.1° = -18.9° 121.1° Min. Southern -23.44° - 5.145° = -28.585° 140.8° Maj. Southern   My "SunMoon Polar Applet" is calculating the sunrise/sunset (as usual in astronomy) at an altitude of -0.83°, and the moonrise/moonset at an altitude of +0.13°. The data computed by the applet were exported the the Java console and sorted by a spreadsheet program.   The observer is located at the centre of his "celestial sphere" with zenith Z above his head and the horizon N-E-S-W. The Sun, Moon or any other celestial body can be identified by the two coordinates altitude (elevation) h and azimuth az (horizontal coordinates). Altitude is the angular distance above the horizon (0 < h < 90°), and azimuth the angular distance, measured along the horizon, eastwards from the north point N in nautics (0 < alpha <360°), or westwards from the south point S (in astronomy). 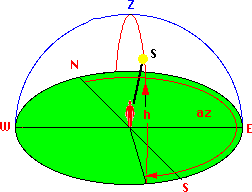More about celestial coordinates. How to get the applet version for offline use

Web Links

Stonehenge (Martin Doutré) Archaeocosmology (Victor Reijs) The Lunar standstill Season

Bücher

Drößler, Rudolf: Astronomie in Stein. Archäologen und Astronomen enträtseln alte Bauwerke und Kultstätten. Lizenzausgabe Panorama Verlag, Wiesbaden, o.J., ISBN 3-926642-25-4. Krupp, Edwin C.: Astronomen, Priester, Pyramiden. Das Abenteuer Archäoastronomie. Beck'sche Verlagsbuchhandlung, München 1980, ISBN 3-406-07601-7. Cornell, James: Die ersten Astronomen. Eine Einführung in die Ursprünge der Astronomie. Birkhäuser-Verlag, Basel 1983, ISBN 3-7643-1379-X. Michell, John: Sonne, Mond und Steine. Ein kleiner geschichtlicher Abriss der Astro-Archäologie. Der grüne Zweig 156. © 1977, 1989 John Mitchel, verlegt durch Werner Piepers Medienexperimente, Löhrbach, ISBN 3-925817-56-5.

Please visit my

GeoAstro Applet Collection

Last modified: 2023, Oct 07