Sun-Earth Distance Applet

The applet is computing the apparent distance of the Earth from the Sun (kilometers and Astronomical Units) using the 409 most important of 997 terms of the VSOP87 planetary theory. In 1850 to 2050, the mean absolute error of the Sun-Earth distance, compared with MICA, is 1.9·10^-7 AU = 28 km, using the conversion 1 AU = 149,597,870 km (details below).
The times of perihelion and aphelion are accurate within about 0.5 hour, and the right ascension and the declination (using fewer terms) are accurate within about 1''.

Select "Anomalistic" from the "Details" menu:

The anomalistic period of the Earth is the time that elapses between two passages at its perihelion. There are large deviations of the interval between perihelion passages (anomalistic period), caused by the Moon deforming the path of the Earth's center (Meeus).

more details below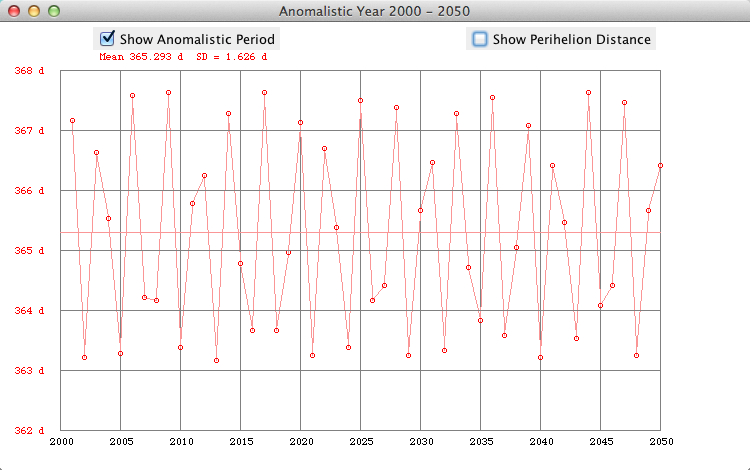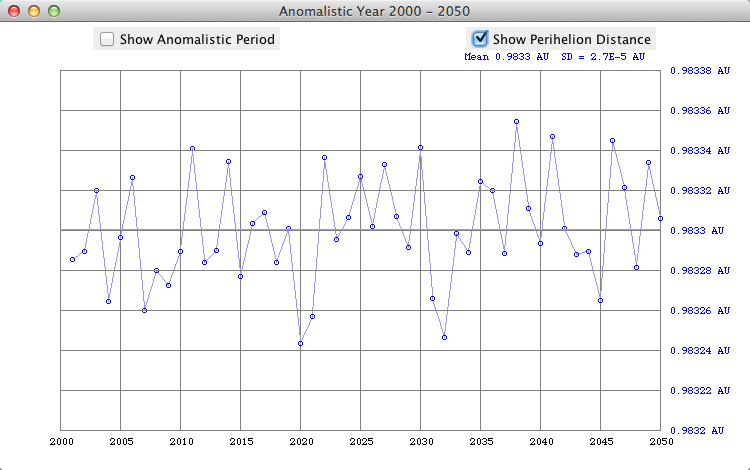

Select "Data Table" from the "Details" menu:

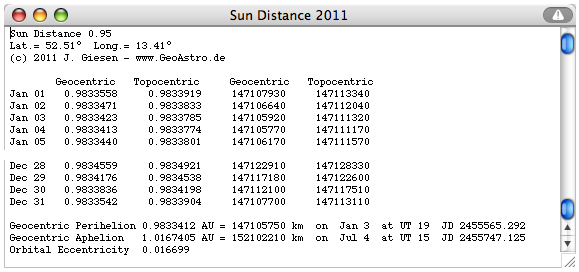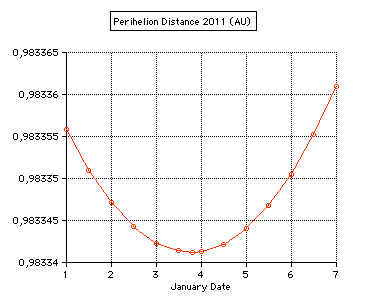Perihelion 2011 occurs on Jan 3 at 19 UT (0.9833412 AU).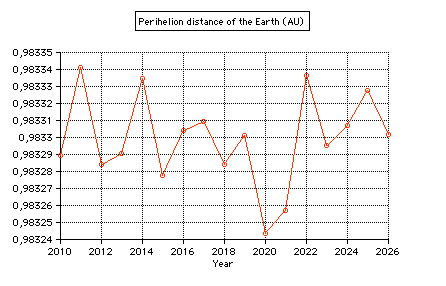

Geocentric perihelion distance 2010 - 2026
computed by MICA (Multiyear Interactive Computer Almanac by US Naval Observatory)

2010 - 2026	Distance / AU	Distance / km
Mean	0.983,299,155	147.099,459
Minimum	0.983,243,565	147,091,143
Maximum	0.983,341,273	147,105,760
Max. - Min.	0,000,097,708	14,617
(Max-Min)/Mean	0.010 %
Stand. Dev.	0.000,026,692	3.993
Stand. Dev.	0.0029 %

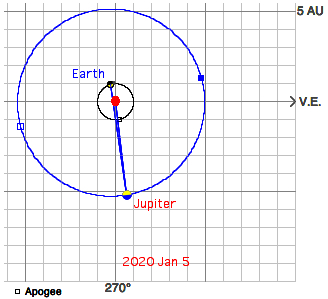The small perihelion distance of the Earth in 2020 and 2021 is due to the conjunctions of Jupiter with the Sun (2019 Dec 27, 2021 Jan 29).

Perihelion occurs between Jan 2 and Jan 05 (mean date is Jan 4.0):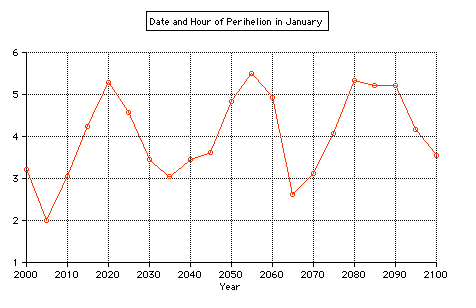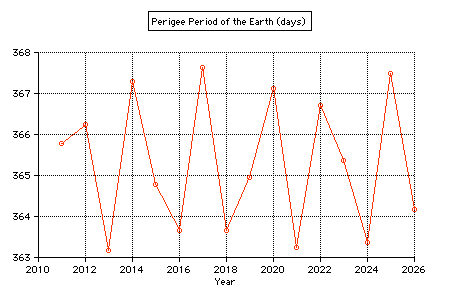
Date of Earth Perihelion

2010 - 2026	Anomalistic Year / days
Mean	365.294
Minimum	363.167
Maximum	367.625
Max. - Min.	4.458
(Max-Min)/Mean	1.22 %
Stand. Dev.	1.636
Stand. Dev.	0.45 %

The ecliptical longitude of the perihelion is advancing by about 3.3° from 1900 to 2100, making one complete cycle in 22,000 to 26,000 years: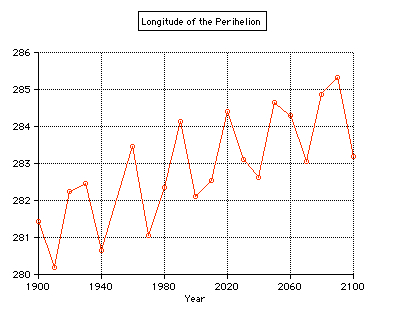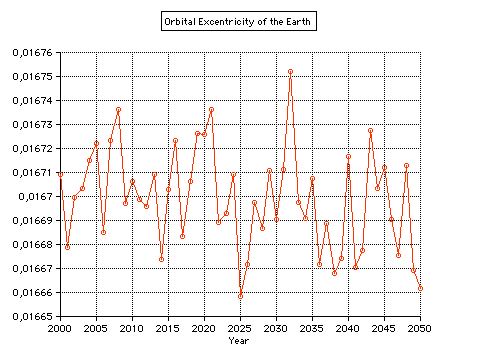
Longitude of Perihelion

2000 - 2050	excentricity
Mean	0.0166988
Minimum	0.0166584
Maximum	0.0167521
Max. - Min.	0.000094
(Max-Min)/Mean	0.56 %
Stand. Dev.	0.000021
Stand. Dev.	0.13 %

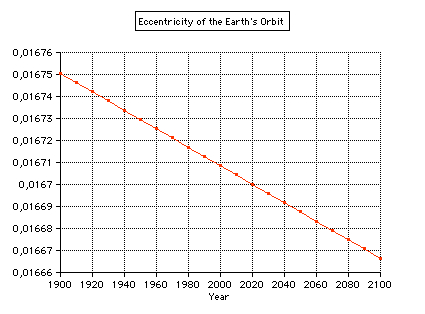The eccentricity of the Earth's orbit 1900 - 2100 according to Meeus (Astronomical Algorithms, Willmann-Bell) is decreasing by 0.000,042 per century (0.0167,086 in 2000).

In 29,450 there will be a minimum of 0.002281: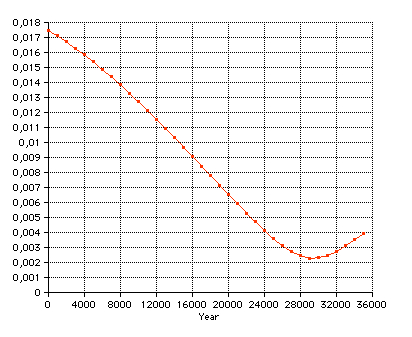

earth orbital eccentricity minimum

More details about long-period variation of the Earth's eccentricity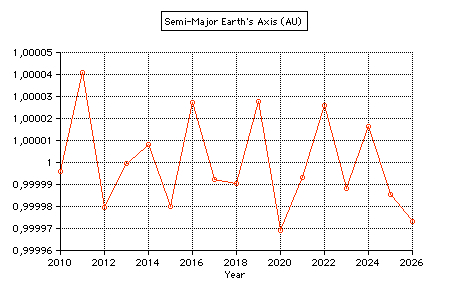

semi major axis earth

Select "Difference" from the "Details" menu:
Showing the second differences d_n of daily distances r_n:
d_n = (r_n+1 - r_n) - (r_n - r_n-1) = r_n+1 - 2r_n + r_n-1
which is an approximation of the second derivative of the r(t) function. It is about zero near the equinoxes where the orbit is almost circular (d_n=0).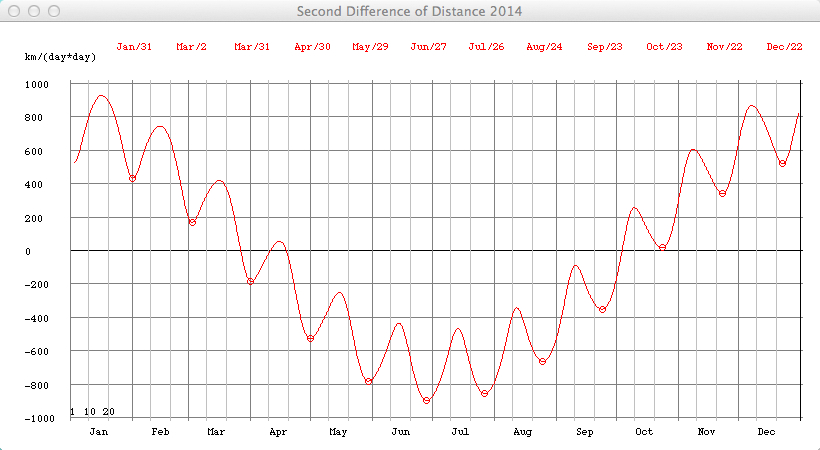

curvature New Moon

The local minima of d_n occur at (near) New Moon.

Select "Orbit" from the "Details" menu: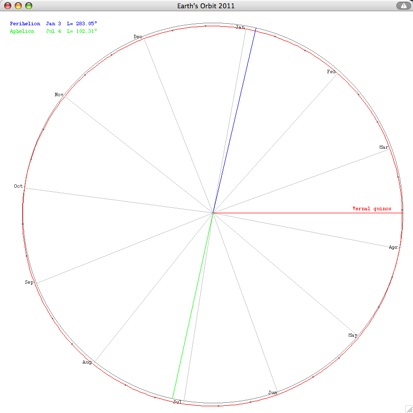

earth orbit around the sun

An eccenticity of 0.0167 and a radius of 380 pix yields a difference between perihelion and aphelion distance of 12 pix.

Marks for the date of the month:

orbit date

This checkboxes is showing the magnified radius (magenta),
concentric gray circles at 0.995 AU, 1 AU, and 1.005 AU

local radius

The local radius (cyan) is computed from 3 adjacent points P_n-1, P_n, P_n+1, using rectangular coordinates computed from the radius r and the ecliptical longitude L.
Cyclic variations is due to the Eart's moon. Local minima occur at new moon.

VSOP Theory

VSOP 87D: heliocentric ecliptic spherical coordinates for the equinox of the day

The VSOP theorie is computing the Sun-Earth distance R from the Julian Day JD by the sum of series R₀, R₁, R₂, R₃, and R₄:

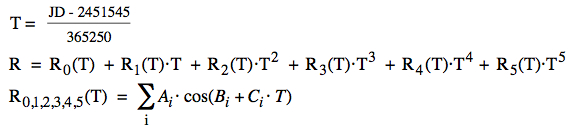The coefficients A_i of R₀ (526 terms) behave like this (in units of AU):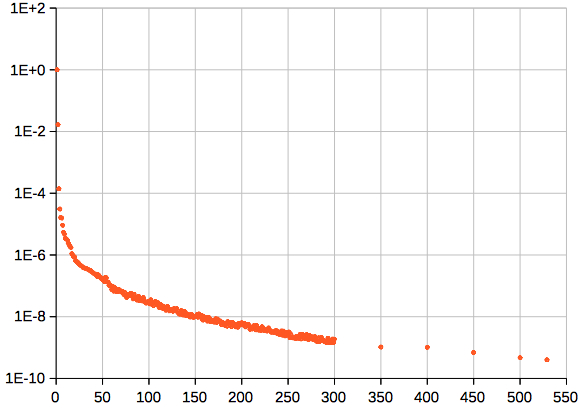

Mean absolute error of R (in units of AU), 1900-2050: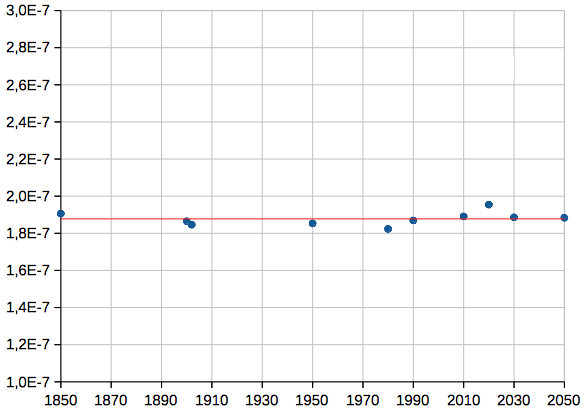

Above: mean error (12 positions per year), and standard deviation:
(1.87 ± 0.80)·10^-7 AU, or (28 ± 12) km

Perihelion of the Earth:

There are large deviations of the interval between perihelion passages of the Earth (anomalistic period), caused by the Moon deforming the path of the Earth's center with respect to a rigorously elliptical orbit [mean perihelion] (Meeus).

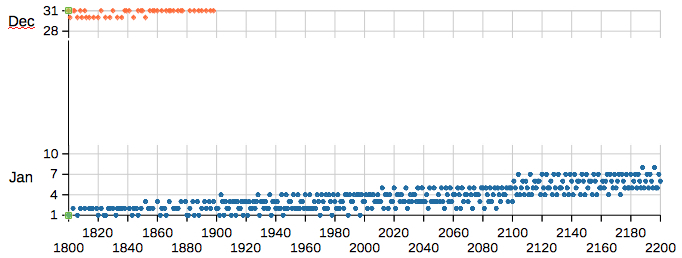The last time of perihelion in December was in 1898, on December 31 at 21 UT.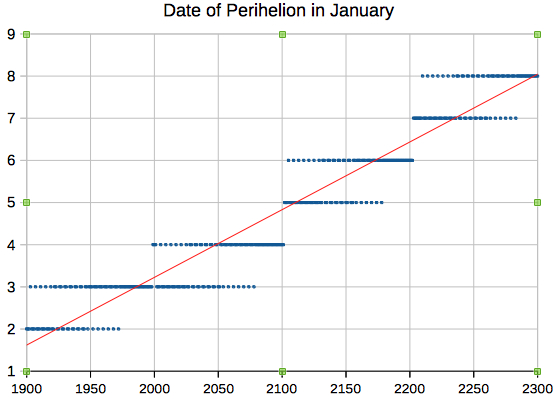

The date of the mean perihelion, computed by Meeus' algorithm (Meeus), is increasing by about 1.6 days per century, from December 26-28 near 1600 to January 10-13 near the year 2500.