Saros-Inex Panorama

Prof. G. van den Bergh investigated the period of 358 lunations or 388 1/2 draconic months in his classic work "Periodicity and Variation of Solar (and Lunar) Eclipses" (1955), calling it the inex. ( "Saros, Inex and Eclipse cycles" by Felix Verbelen). Year 2000: Synodic Month (lunation) new moon to new moon 29.5305889 d * 358 = 10,571.951 d app. 29 years, minus 20 days Draconic Month node to node 27.2122208 d * 388 1/2 = 10,571.948 d app. 29 years, minus 20 days As a consequence of the fraction 1/2 eclipses in an inex series take place alternately at the one and the other node (unlike eclipses in a saros series). Therefore an eclipse in the northern hemisphere of the Earth will be followed, after 1 inex, by an eclipse in the southern hemisphere. Van den Bergh found that the interval T of time between two solar (or lunar) eclipses can be established from the simple formula: T = m*Inex  +  n*Saros Inex= 358 synodic months (10571.95 days) Saros = 223 synodic months (6585.32 days, 18 years and 10 or 11 days and 8 hours ) m and n are integral numbers (zero, negative or positive). He arranged 8000 solar eclipses in a soros-inex panorama, grouping the eclipses column by column according to saros intervals, and line by line according to inex intervals. One step down in the panorama means one saros later, and one step to the right means one inex later. Successive eclipses (in time) don't bear successive saros numbers.   The lifetime of saros and inex series The cycles do not coincide exactly. Calculating the misfit of the coincidences (year 2000): saros inex 27.212221 d * 242 = 6,585.357 d 29.530589 d * 223 = 6,585.321 d 6,585.357 d - 6,585.322 d = 0.036 d 0.035 * 360° / 27.212 = 0.478° 29.5305889 d * 358 = 10,571.951 d 27.2122208 d * 388.5 = 10,571.948 d 10,571.951 d - 10,571.948 d = 0.003 d 0.003 * 360° / 27.212 = 0.040° Assuming that a solar eclipse is still possible at a distance of 18.4° from a node (example), the number of saros periods in a series would be 2*18.4° / 0.478° = 77 In fact, each saros series lasts 12 to 15 centuries, and produces 69 to 86 eclipses, separated by one saros period (6585.32 days). Inex series have a longer lifetime than saros series, because the shift of the moon with respect to the node of its orbit is much smaller for the inex (0.040° per cycle) than for the saros (0.478° per cycle), and the inex period (29 years) is longer than the saros (18 years). Assuming again that a solar eclipse is still possible at a distance of 18.4° from a node, the number of inex periods in a series would be 2*18.4° / 0.040° = 920 which is a lifetime of 920*29 years = 26,680 years. As Meeus (Mathematical Astronomy Morsels III) is pointing out, the lengths of the synodic, draconic and anomalistic months are subject to long time alterations, and the effective lifetime of an inex series cannot be calculated in this simple way. A saros-inex panorama has been produced by Luca Quaglia and John Tilley in the form of a Microsoft Excel file. It shows 61775 solar eclipses from -11000 to +15000 organised by saros series (columns, -290 to 620) and inex series (rows, 60 to 98). The panorama is supplied on four worksheets. These can be printed and glued together to form a large display. Each cell of the spread sheet reperesents an eclipse of the Sun: partial total annular annular/total Details of the saros series 145 and 146

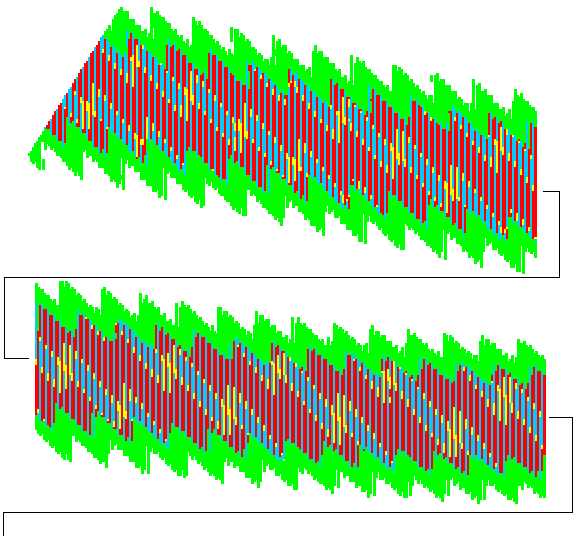
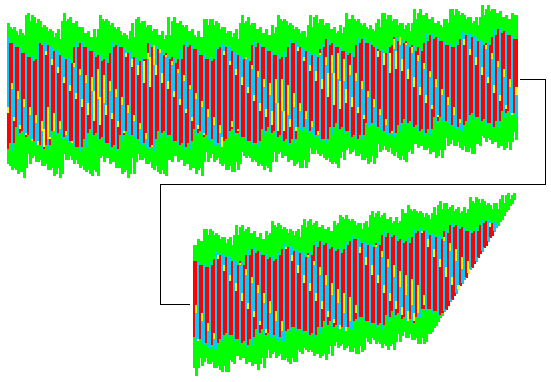
The Example shows a small part of the saros-inex panorama. Saros 145, inex 38 is the total eclipse of 1999, Aug 11 (greatest magnitude at 11:03 UT, 45.1N 24.3E, visible in Europe):

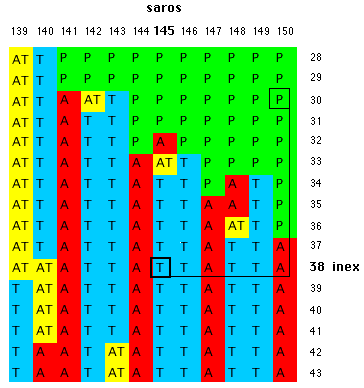
The succeeding eclipse of inex 38 is on 2028 Jul 22 at 02:55 T 146 -0.606 1.056 15.6S 126.8E 53 230 05m10s To get the next eclipse (in time) of 2000 Feb 05 (which is partial), we have to move 5 columns to the right and 8 rows upward: 5 inexes - 8 saroses = 5*358 - 8*223 = 6 lunations

Cycle	Saros-Inex Combination	Lunations	Interval of Time
Semester	5 i - 8 s	6	177.18 d 0.485 y	Two successive lunar or solar eclipses at alternate lunar nodes
Saros	s	223	6,585.32 d 18.03 y	Similar solar eclipses spaced about 120º apart in terrestrial longitude.
Inex	i	358	10,571.95 d 28.945 y	Similar solar eclipses at the same terrestrial longitude but opposite latitudes. (?)
Exeligmos (Triple Saros)	3 s	669	19,755.96 d 54.090 y	Similar solar eclipses at approximately the same terrestrial longitude.

More cycles: A Catalogue of Eclipse Cycles (Robert Harry van Gent)

Details of the saros 145 and 146