Home Site Map Search

GeoAstro Applets

Astronomy

Chaos Game

Java

Miscel- laneous

  Atmospheric Refraction Applet
Apparent Flattening of the Sun

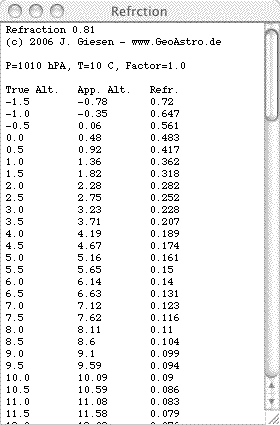
The true elevation angles of the Sun are not corrected for atmospheric refraction, which is bending the light while passing through the Earth's atmosphere. The effect of refraction depends on atmospheric conditions (pressure, temperature, relative humidity) and on the wavelength. For mean conditions (P=1010 hPa, T=10°C, yellow light) the refraction R is calculated by Saemundsson's formula (Meeus, Astronomical Algorithms): 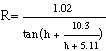h is the true (airless) elevation in degrees, R is in minutes of arc. The apparent (observed) elevation is h+R. Taking into account variations of the pressure P (hPa) and the temperature T (°C), R should be multiplied by the approimate faktor (Meeus, Astronomical Algorithms): The amount of refraction increases by about 1% for every 3 °C colder, and by about 1% for every 9 hPa higher pressure. Extreme values of the pressure are 1086 hPa and (non-tornadic) 870 hPa As a consequence of the refraction, the solar disc seems to be flattened near the horizon. At runrise, when the apparent lower limb is just on the horizon, the apparent vertical diameter of the Sun is 26.9', and the apparent flattening ratio is 26.9'/32' = 0.84 For my photo the ratio of flattening is about 0.86. More photos and Dia Show

Select "Graph: Refraction" from the "Details" menu:

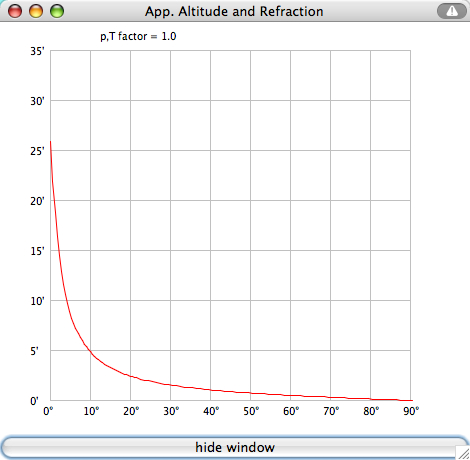
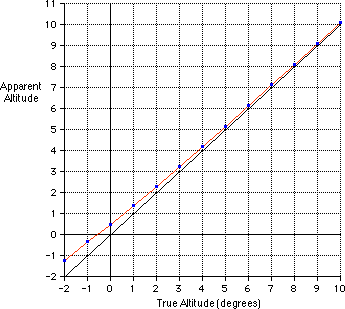
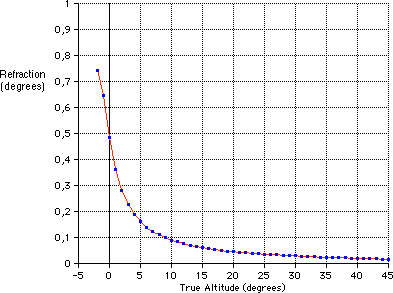
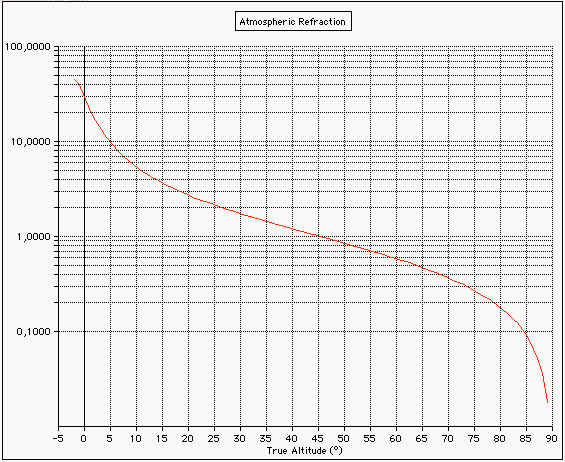
Altitude correction (arcminutes): apparent alt. = true alt. + correction.

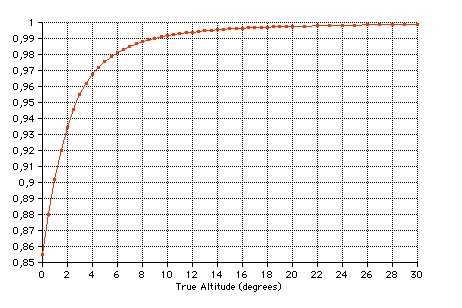
Apparent flattening ratio of the Sun.

Web Links

Flattening of the setting Sun Optical Phenomena of Ducts Weather Photography: Flattening of sun and moon Atmospheric Extinction and Refraction The Moon Illusion Atmospheric Refraction (Wikipedia) Atmospheric pressure (Wikipedia) Astronomical Refraction: Computational Method for all Zenith Angles

(c) 2006-2023 J. Giesen

Updated: 2023, Oct 06