|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Gambler's Ruin Applet
|
A gambler
starts with a stake of size S.
He repeatedly plays a fair game, with 0.5 probability of winning or losing 1 dollar, until his capital reaches the value M or until going broke (capital 0). |
| button starting a single game, the diagram is showing the current capital button to stop the game |
|
| select the value S
of the initial stake |
|
| select the value M
of the final capital the player tries to reach |
Statistical analysis:
| button starting a set of N games |
|
| the numbers N of games can be selected from the menu |
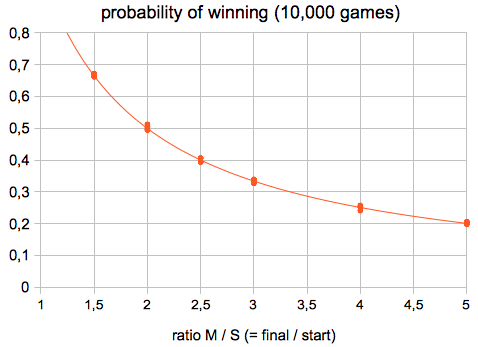
The probability of winning a capital M starting
expected duration of a fair gambling game
P = S / M
expected duration of a fair gambling game
If the gambler starts with S dollars and plays until he is broke (lost) or has a capital of M dollars,
he can expect n = S·(M-S) steps
expected duration of a fair gambling gam
expected duration of a fair gambling
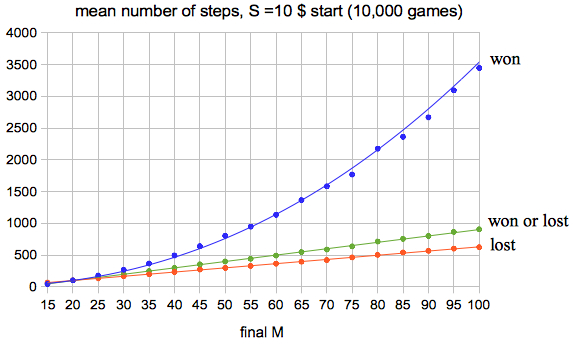
The green line is computed from the blue and red one by:
n = Pwon·nwon + Plost·nlost = (S/M)·nwon + (1-S/M)·nlost
which agrees with n= S·(M-S)
Updated: 2023, Oct 06