Sieve for Prime Numbers by a Parabola
| The page "Crible
géométrique (hyperbole)" by Jean-Paul
Davalan inspired me to write the interactive Java
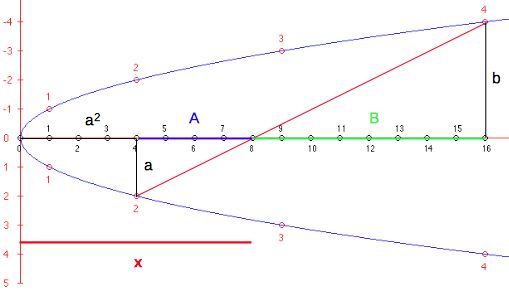
applet below. On the rectangular parabola x = y2 the points { (i2 , i), i integer, i >1 } and { (k2 , -k), k integer, k >1 } are marked and joined by a line crossing the horizontal x axis. The points of intersection are (i · k, 0), indicaomittingting the product, the prime numbers {2, 3, 5, 7, 11, 13, 17, 19, 23,
29, 31, 37, 41, 43, 47, ...}
This sieve was created by Yuri
Matiyasevich and Boris Stechkin.if i≠1 or k≠1.
The construction also interprets the multiplication of real numbers. |
 |
Select the maximum value of x on the horizontal axis. |
 |
Select the number of lines to be drawn
from each point on the parabola. |
| Pressing the "clear" button erases all
lines. Click on a number on the parabola (with cursor set to cross hair) to draw lines, or press "draw lines" to redraw all. |
|
| You can add the lines using the click mode. |
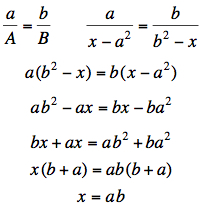
|
|
| A
visual Sieve for Prime Numbers (Yuri MATIYASEVICH
and Boris STECHKIN) A Parabola Sieve for Prime Numbers (Wolfram) Catching primes (Abigail Kirk) Le crible géométrique de Matiiassevitch (Therese Eveilleau) |
2017-2023 J. Giesen
updated: 2023, Oct 06