Home Site Map Search

GeoAstro Applets

Astronomy

Chaos Game

Java

Miscel- laneous

Java applet calculating local conditions for crescent moon sighting

The Islamic calendar (Hijri calendar) is a purely lunar calendar. consisting of twelve alternating months of 30 and 29 days, with the final 29 day month extended to 30 days during leap years. Islamic months begin at sunset on the day of visual sighting of the lunar crescent (hilal). See example 2006. New Moon is defined as the Moon's phase when it is at the same celestial longitude as the Sun (conjunction) and thus totally unilluminated as seen from the Earth.

Location:	Select a location from the menu list, enter Latitude and Longitude manually (decimal degree values and press return key), or simply click the word map (dont forget to adjust the time zone).
	Look up your coordinates: in the location database (Heavens Above): 2 million towns and villages world-wide. Enter latitude in decimal degrees and press return key, enter longitude in decimal degrees and press return key.
Time Zone	Find the time zone (and coordinates) of cities worldwide: The World Clock Interactive time zone map of countries around the world.
Key commands:	You may use the keys "m", "d", "h", "n" to increase the month, date, hour, or minute, or Shift key and "m", "d", "h", "n" to decrease the month, date, hour, or minute ! Click the applet background first !
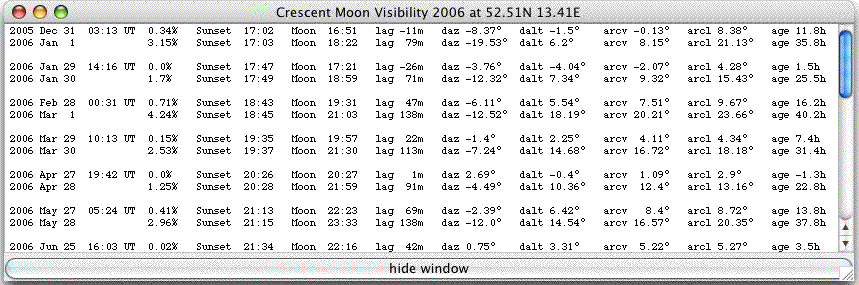
Details menu	Data: Solar and lunar data are computed. New Moon: Date and time of new Moon for the year selected. daz, dalt, arcl, arcv: Computing quantities to predict lunar crescent visibility. Crescent map: not yet implemented online...

Example: New Moon on 2006 May 27 at 5:24 UT
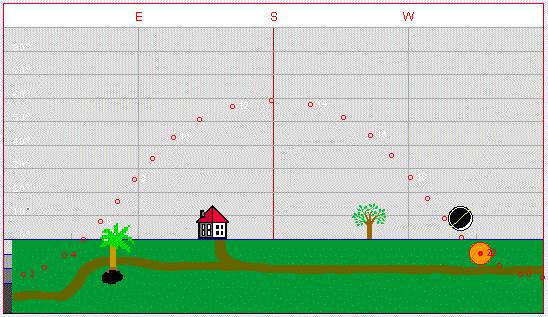
Berlin 2006, 52.51N, 13.41E, UT+2h, May 28

sunset moonset app. altitude of the Moon's lower limb at sunset (DALT) app. altitude of the Sun at 22:00 app. altitude of the center of the Moon at 22:00 geocentric elongation at 22:00 age of the Moon at 22:00 illuminated fraction of the Moon at 22:00:

21:15 23:33 14.6° -6.1° 9.2° 20.7° 1d 14h 36m 3.1%

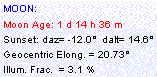
The time the Moon first becomes visible after the New Moon depends on many factors. The various effects are the geometry of the Sun, Moon, and horizon; the width and surface brightness of the crescent; the absorption of the Moon's light and the scattering of the Sun's light in the Earth's atmosphere; and the physiology of human vision.

 

optical aid	< 15 h	< 18 h	< 21 h	< 24 h

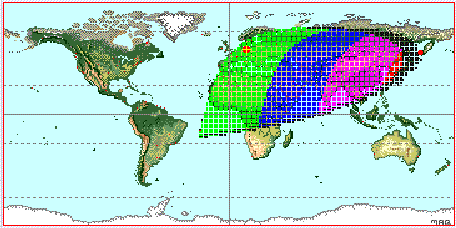
2006, Apr 27

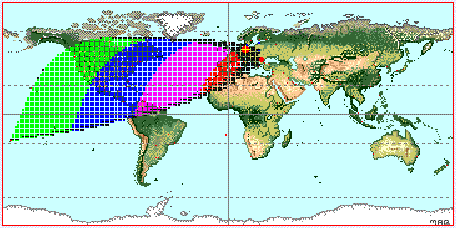
2006, May 27

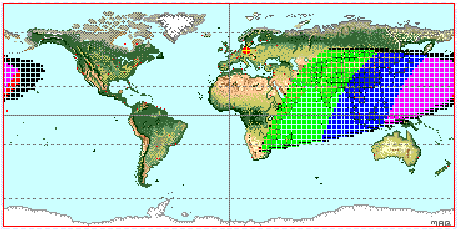
2006, Jun 25

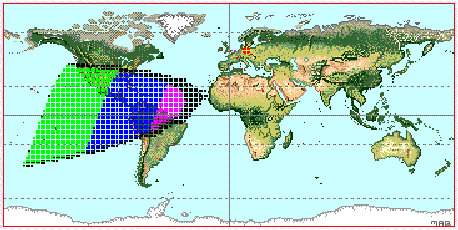
2006, Jul 25

Basic variables:

	Sunset	the times when the upper edge of the disk of the Sun is on the horizon, the true altitude of the center of the Sun is -0.83°.
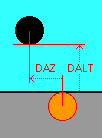
	DALT	apparent altitude of the lower limb of the moon (with topocentric parallax and refraction corrections), at moment of sunset (or sunrise)
	DAZ	moon azimuth minus sun azimuth, at moment of sunset (or sunrise)
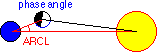
	ARCL	arc of light, the angle subtended at the center of the earth by the center of the moon and the center of the sun
	ARCV	is the geocentric difference in altitude between the centre of the Sun and the centre of the Moon for a given latitude and longitude ignoring the effects of refraction
%		illuminated fraction of the lunar disk, depenging on the selenocentric phase angle
Lag		Time in minutes from sunset to moonset

The angles ARCL ARCV and DAZ are related by the equation:

cos(ARCL) = cos(ARCV) * cos(DAZ )

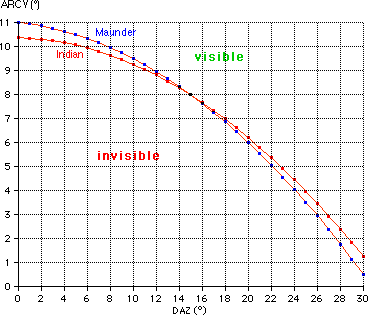
The chart is using the formulas (given by Yallop):

Maunder: ARCV = f(DAZ) = 11 - DAZ/20 - DAZ²/100

Indian: ARCV = f(DAZ) = 10.3746 - 0.0137*DAZ - 0.0097*DAZ²

If ARCV>f(DAZ) then the crescent Moon is visible, if ARCV < f(DAZ) it is not visible.

On my Apple PowerPC G5 (1.8 GHz) it takes about 90 seconds to create a visibility map

Web Links

Crescent Moon Visibility (USNO) Crescent Visibility 2006 (South African Astronomical Observatory) Moonsighting Committee Worldwide Islam, Astronomy, Hilal (Crescent Moon), New Moon, and Cyberspace A Method for Predicting the First Sighting of the New Crescent Moon (B. D. Yallop), PDF First Visibility of the Lunar Crescent (Caldwell, Laney), HTML First Visibility of the Lunar Crescent (Caldwell, Laney), PDF Computational Astronomy and the Earliest Visibility of Lunar Crescent (M. S. Qureshi), PDF Seeking Thin Crescent Moons (R. W. Sinnot) Global First Sighting of New Crescent Moon information (H.M. Nautical Almanac Office) On the Crescent's Visibility (S. K. Abdali) PDF Crescent Sighting Frequently Asked Questions Committee For Crescent Observation Intl. Rise, Set, and Twilight Definitions (USNO) A Closer Look at Rise, Set and Twilight Islamic Calendar based on predicted lunar visibility Islamic calendar (Wikipedia) Islamic-Western Calendar Converter Islamic calendar Calendar Converter (fourmilab)

Last Modified: 2023, Oct 06

© 2006-2023 J. Giesen