Details: series
expansion, Newton's method
Movie
of
elliptical motion
Plots
of
elliptical Kepler motion
Circumgerence
of an ellipse
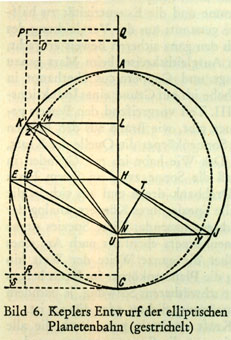
E. Zinner: Astronomie, Alber, Freiburg/München 1951.
In 1609 Kepler published his work Astronomia
Nova, containing the first (and the second)
law of planetary motion: Between 1617 and 1621 Kepler wrote Epitome
Astronomiae Copernicanae, the first
astronomy textbook based on the Copernican model.
Kepler introduced what is now known as Kepler's
equation for the solution of planetary
orbits, using the eccentric anomaly E, and the
mean anomaly M. The term anomaly (instead of angle),
which means irregularity, is used by astronomers
describing planetary positions. The term
originates from the fact that the observed
locations of a planet often showed small
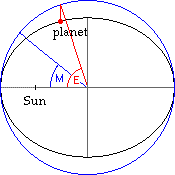
deviations from the predicted data. The mean anomaly M is the angular
distance from perihelion which a (fictitious)
planet would have if it moved on the circle of
radius a with a constant angular velocity
and with the same orbital period T as the real
planet moving on the ellipse. By definition, M
increases linearly (uniformly) with time. Operating with radians Kepler's equation
is: or, using degrees: The equation can be The value of M at a given time is easily
found when the eccentricity e and the eccentric
anomaly E are known. The problem is to find E
(from which the position of the planet can be
computed) when M and e are known. The true anomaly (symbol φ) is the
angular distance of the planet from the perihelion
of the planet, as seen from the Sun. For a
circular orbit, the mean anomaly and the true
anomaly are the same. The difference between the
true anomaly and the mean anomaly is called the JavaScript using
Newton's method: The form is preset to: The results, as shown in the figure
below, are:
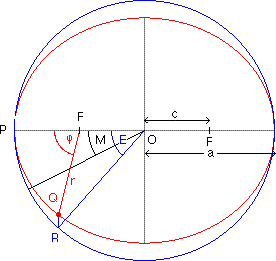
Planets move in elliptical orbits with the sun
at one focus.
![]() derived from Kepler's second law.
derived from Kepler's second law.
Kepler's equation cannot be solved algebraically.
It can be treated by an iteration
methods. One of them is Newton's method, finding
roots of
![]() Equation of
Center C:
Equation of
Center C: eccentricity e=0.5
mean anomaly M=27° or t/T=0.075.true anomaly phi=75.84°
eccentric anomaly E=48.43°
|
An example of a series expansion is: Details: series expansion, Newton's
method
For small eccentricities the mean anomaly M can be used as an initial value E0 for the iteration. In case of e>0.8 the initial value E0=π is taken. function EccAnom(ec,m,dp) { // arguments: } function TrueAnom(ec,E,dp) { K=Math.PI/180.0; }
function position(a, ec,E) { // a=semimajor axis, ec=eccentricity, E=eccentric anomaly } (c) 2006-2016 J. Giesen
Updated: 2016, Jan 05 |