Freiburger Münster
Nachweis der Erdroration durch Fallversuche
| |
| Das Freiburger Münster gehört
zu den wenigen großen gotischen Kirchenbauten, die noch im
Mittelalter vollendet wurden. Auch sein prachtvoller
Westturm wurde bereits um 1330 fertiggestellt. In der Turmhalle finden sich auf dem Boden zwei Markierungen, die auf Fallversuche hinweisen. Eine dieser Marken ist der Lotpunkt der Turmspitze, die andere ist der Punkt, in dem ein von der Turmspitze frei fallender Körper auftrifft. Der Abstand beträgt 3,1 bis 3,2 cm. Die Differenz der beiden Punkte ist
eine Folge der Erddrehung um ihre Achse.
Die im folgenden hergeleitete Rechnung ergibt für die Ablenkung von der Lotrichtung jedoch nur 1,8 cm, also eine beträchtliche Diskrepanz. Auch bei ähnlichen Fallversuchen in Vergangenheit und Gegenwart sind große Schwankungen der Einzelmessungen aufgetreten. Ein Hauptproblem ist, dass der Körper beim Loslassen ungestört bleibt. Weiter unten sind historische und moderne Fallversuche beschrieben:
>>J'ai essayé la mȇme experience au Panthéon, en 1903, et constaté, par 144 chutes de petites balles d'acier, tombant d'une hauteur de 68 mètres, une deviation de 6 mm 3 vers l'est. Le calcul indiquait 8 mm 1".<< Im Bulletin
de la Société Astronomique de
France von 1903
beschreibt er ausführlich die Versuche, mit dem
Endergebnis:
Seite 334:
8,1 mm liefert auch die Formel (*) weiter unten. Berücksichtigt mann die Luftreibung kann für seine benutzen Stahlkugeln von 15,84 mm Durchmesser und 16,25 g, nehmen Fallzeit und Ostablenkung um 3,9% zu: ∆x=8,4 mm. Es gelten damals wie heute die Worte von Carl Friedrich Gauß, der eine zutreffende Theorie der Fallversuche lieferte (zitiert nach Willerding): ... das die Fallversuche
wenig geeignet sind die Drehbewegungen der Erde
erkennbar zu machen,
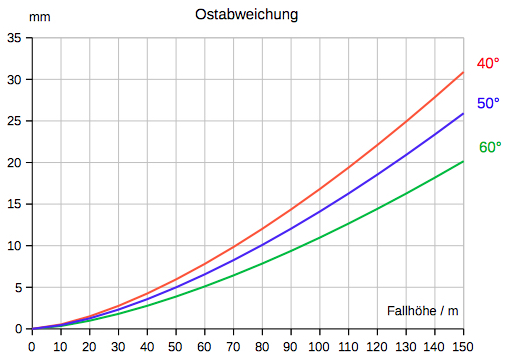
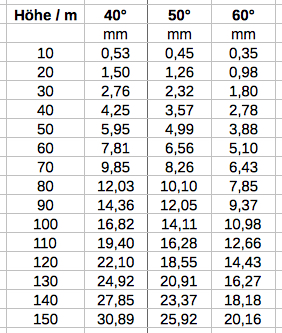
da sie nach den kostspieligsten Zurüstungen doch immer nur höchst rohe Resultate geben können. Das Diagramm zeigt den zu erwartenden
Effekt der Ostabweichung in Abhängigkeit von Fallhöhe
und geographischer Breite:
Herleitung der Ostabweichung
Eine qualitative Erklärung
der Ostablenkung ergibt sich dadurch, dass der Körper
durch die Erddrehung nach Osten beim Loslassen in der
Höhe H wegen seines größeren Drehradius eine größere
tangentiale Geschwindigkeit v1 besitzt als
der Lotpunkt auf dem Boden (v0). Er landet
also östlich des Lotpunktes.
Halbquantitativ kann man rechnen: v1 = cos(φ)·(R+H)·ω
v0 = cos(φ)·R·ω ∆v = cos(φ)·H·ω Mit der Geschwindigkeitsdifferenz
∆v und der Fallzeit T bis zum Boden
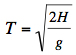 beträgt dann die Ablenkung
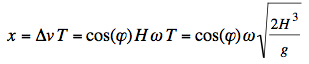 ----------
Das erdfeste Bezugssystem (x,y,z) hat seinen Ursprung auf der geographischen Breite φ, mit der x-Achse nach Osten (senkrecht in die Zeichenebene hinein), der y-Achse nach Norden und der z-Achse radial nach außen, also senkrecht zur Erdoberfläche. Es rotiert wie die Erde mit der Winkelgeschwindigkeit  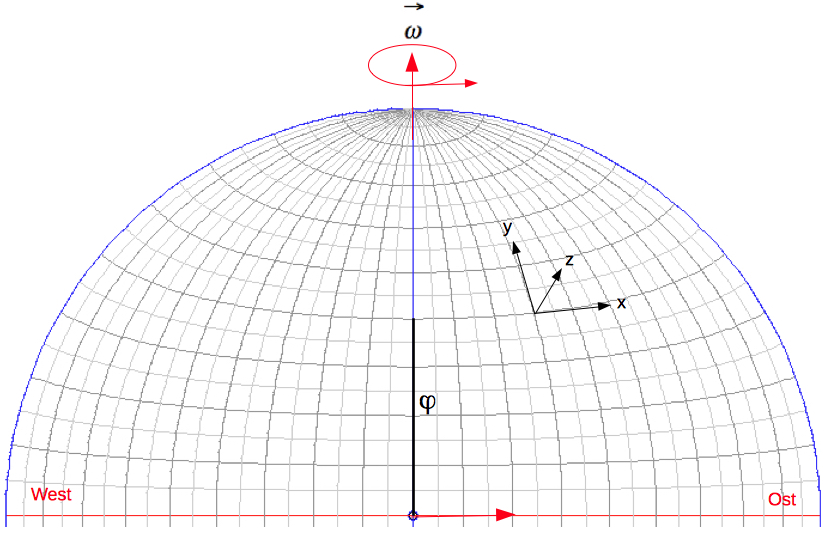 Ein Körper, der sich in diesem
rotierenden System mit der Geschwindigkeit
Die vereinfachte Bewegungsgleichung lautet dann:  Auf der geographischen Breite φ ist: 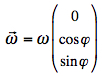  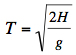 Am Boden ist die Ablenkung dann

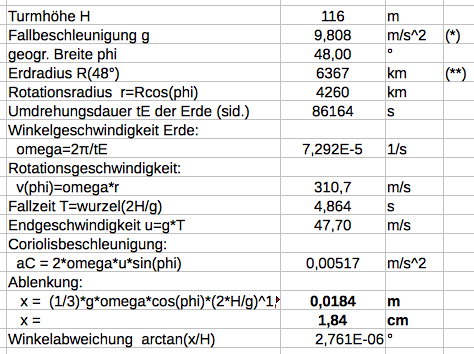
Nimmt man als Höhe der
Turmspitze des Freiburger Münsters H=116 m
an, ergibt sich für die Ostablenkung:
x = 1,84 cm.
 Ohne die
Vereinfachung
die beim
Freiburger Münster nur 0,0024 mm
beträgt und somit nicht
nachweisbar ist.
Auch die Orientierung der Marken ist fraglich. Die Diagonale der Bodenplatten hat die Richtung des Langhauses, die nur wenig (1° bis 2°) von der Ost-West-Ausrichtung abweicht (Karten).   Der Richtung der Markierungen beträgt 42,6° gegen magnetisch Nord, die magnetische Deklination +3° Ost, somit ≈ 46° gegen Nord (ohne Störung durch den Boden). Alternative Herleitung Ein frei fallender Körper
bewegt sich zunächst in guter Näherung auf
einer Keplerschen Ellipse, für die der
Fächensatz gilt (nach Willerding):
----------Fallversuche von Giovanni Battista Guglielmini Seine Ergebnisse
veröffentlichte Guglielmini (1763 - 1817)
im Jahre 1798 auf Italienisch und 1792 auf
Lateinisch. Der Turm
der Asinelli in Bologna ist 97,2 m hoch,
und Guglielmi nutzte eine Fallhöhe von
78,3 m. Um Erschütterungen und Wind zu
meiden, führte er von Juni bis September
seine 16 Versuche nachts durch. Eine
Tabelle der Lateinischen Publikation (S.
78-79) gibt die jeweilige Position des
Fallkörpers am Boden in östlichen und
südlichen Koordinaten an, die aber noch
mit der Position des Lots zu verrechnen
waren.
Einheiten: pollices,
lineas; z.B. 7:5,5 = 7*12+5,6
Linien=89,6 Linien à 2,2558 mm = 202,12
mm)
Als gravierender Mangel führte er diese
Messung jedoch erst 6 Monate später im
Februar aus, mit andersartigen
klimatischen Auswirkungen auf die Statik
des Bauwerks.Das Diagramm zeigt seine 16 Ergebnisse nach Verrechnung mit der Lotposition in der Einheit Pariser Linien:  5 5Ohne den Ausreißer ('flante vento', windig) ergibt sich als Mittelwert ( x = 7,4 ± 1,9
y = - 5,0 ± 1,4 x = (16,7 ± 4,4) mm y = - (11,2 ± 3,1) mm Die Rechnung mit
Fallhöhe 241 Pariser Fuß =
241*12*12*2,2558 mm = 78,3 m, Breite
für Bologna 44,5°, g=9,806 m/s^2
liefert als Ostablenkung
x = 10,9 mm
Mit seiner unzutreffenden Theorie berechnet Guglielmini x=7,581 Linien = 17,1 mm ---------- Fallversuche von Johann Friedrich Benzenberg Der Düsseldorfer
Physiker, Astronom und Geodät Johann
Friedrich Benzenberg (1777 - 1846)
führte 1802 Fallexperimente im Turm des
Hamburger Michel aus, sowie 1804 in
einem Kohleschacht der Zeche Trappe in
Wetter-Schlebusch bei Hagen. Seine
Experimente, die Theorie und frühere
Versuche beschreibt er sehr ausführlich
auf 543 Seiten und 7 Tafeln: (J. F. Benzenberg:
Versuche über das Gesetz des freien
Falls.
Hamburger Michel
Juli bis Oktober 1802 Mein Bild zeigt die
Verteilung von 31 Messungen in Pariser
Linien mit Mittelwert (

Die Werte in Pariser
Linien erstrecken sich von 14,8 nach
Westen bis 21,5 nach Osten mit dem
Mittelwert 4,0 Ost:
x = 4,0 ± 8,7
sowie von 17 Süd bis
10,5 Nord mit dem Mittelwert 1,5 Süd
y = - (1,5 ± 6,3)
Umgerechnet in mm (1
Pariser Linie=2,2558 mm) :
x = (9,0 ± 19,7)
mm
y = - (3,4 ± 14,1) mm Mit der Fallhöhe 76,34
m (235 Pariser Fuß), Breite 53,55° und
g=9,814 m/s^2 berechnet man als
Ostabweichung
x = 8,69
mm
Zeche Trappe Oktober 1804 Benzenberg verwendet
Kugeln aus einer Legierung von Blei und
Zinn mit Durchmesser 16 Pariser
Linien und 17 Lot Gewicht (3,6 cm und
0,235 kg).
Mein Bild zeigt die Verteilung von 29 Messungen in Pariser Linien mit Mittelwert ( 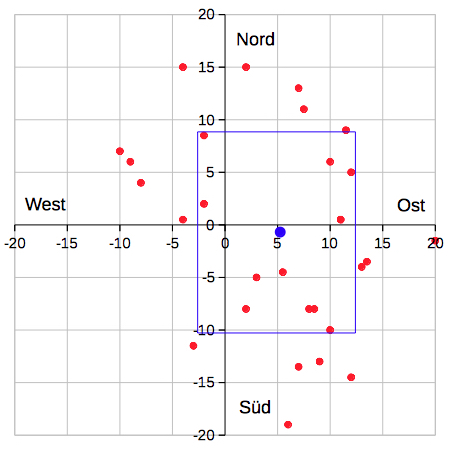
Die Werte erstrecken
sich von 10 nach Westen bis 20 nach
Osten mit dem Mittelwert 5,1 Ost:
x = (5,1 ± 7,6)
sowie von 19 Süd bis
15 Nord mit dem Mittelwert 0,7 Süd
y = - (0,7 ± 9,4)
Umgerechnet in mm (1
Pariser Linie=2,2558 mm) :
x = (11,5 ±
17,1) mm
Mit der Fallhöhe 85,11 m (262 Fuß),
Breite 53,55° und g=9,814 m/s^2
berechnet man als Ostabweichungy = - (1,6 ± 21,2) mm x = 10,75
mm
>>Als er
[Benzenberg] 1815 nach Paris reiste
und Laplace traf, sagte dieser,
"dass er die Wahrscheinlichkeit der
Schlebuscher Versuche berechnet und
gefunden hätte, dass man 8000 gegen
1 wetten könne, dass die Erde sich
drehe".<< (zitiert nach M. Hagner,
S. 76)
Fallversuche von Ferdinand Reich Ferdinand Reich (1799 -
1882) nutzte bei seinen Experimenten im
August und September 1831, die er als
Professor für Physik an der Bergakademie
Freiberg durchführte, den
Drei-Brüder-Schacht im Freiberger
Revier.
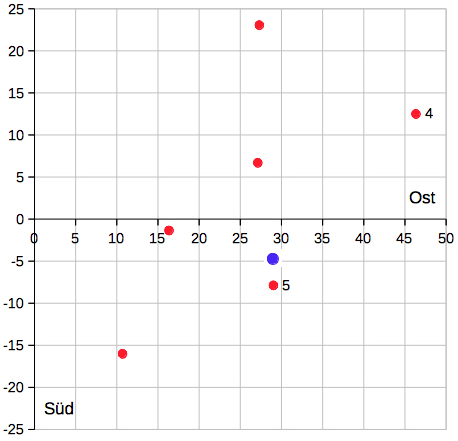 Insgesamt wurden 106
Versuche in 6 Reihen durchgeführt, mit
zwei verschiedenen Verfahren des
Loslassens: Zange bzw. Ring, durch den
die vorher erwärmte Kugel beim Erkalten
fällt.
Die Kugeln hatten im Mittel 4,034 cm Durchmesser und 270,45 g Masse (Dichte 7,878 g/cm^3). Bei unterschiedlichen Gewichten für die Mittelwerte der einzelnen Reihen wurden diese "nach den Regeln der Wahrscheinlichkeitsrechnung" zu einem Gesamtmittelwert verrechnet. Hierbei hatte Reihe 5 für die östliche Abweichung des höchste Gewicht, die Reihen 4 und 5 für die südliche Abweichung: x = (28,396 ±
2,703) mm
Dank enormer Sorgfalt gelingt eine sehr
gute Bestimmung der Ostablenkung.y = - (4,374 ± 2,7) mm Mit Fallhöhe 158,5
m, Breite 50,89° und g=9,810 m/s^2
berechnet man
x = 27,6 mm
Berücksichtigung
der Luftreibung
Mit den Kugeln Reichs beträgt der relative Unterschied ∆T/T der Fallzeit mit und ohne Luftreibung 3,5 % bei 158,5 m Höhe. 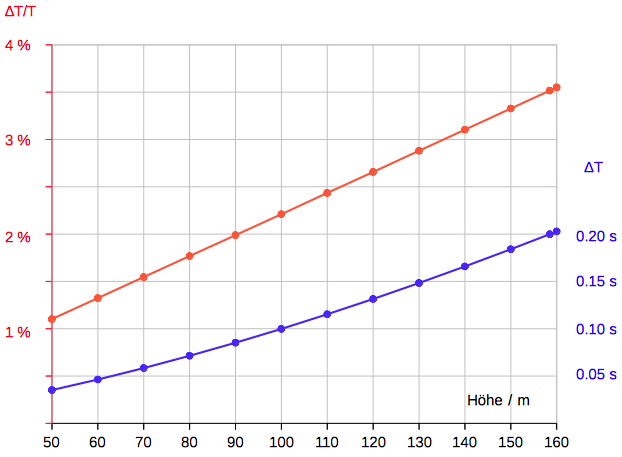 Moderne
Wiederholungen
Draszow, Backhaus (Koblenz 1996) Die Fallversuche im
Rahmen einer Staatsexamensarbeit
fanden im Treppenhaus des Gebäudes der
Universität Koblenz statt, Fallhöhe
16,51 m, Breite 50,34°, 109 Versuche.
Die Einzelwerte der beobachtete Ostabweichung lagen zwischen 5,5 mm West 85 mm Ost mit dem östlichen Mittelwert x = (1,8
± 0,3) mm
berechnet:
x = 0,94 mm
Südabweichungen
wurden beobachtet zwischen 4
mm Nord und 5,5 mm Süd mit dem
südlichen Mittelwert:
y = -
(0,9 ± 0,2) mm
Bähr u.a.
(Bremen 2003)
Ein
studentisches Projekt an
der Freien Universität
Berlin wurde im Zentrum
für angewandte
Raumfahrttechnik und
Mikrogravitation (ZARM,
Fallturm Bremen)
durchgeführt.
Als Abwurfvorrichtung der Kugeln (8 mm) dienten Elektromagnete. Fallhöhe 119 m, Breite 53,11°, 120 Messungen: Die
Einzelwerte der gemessenen
Ostabweichungen lagen
zwischen 4 mm und 68 mm
mit dem Mittelwert
x = (26,6
± 10,7) mm
x = 17,1 mmberechnet:
Die
gemessenen Südabweichungen
lagen zwischen 18 mm Nord
und 45 mm Süd mit dem
südlichen Mittelwert:
y = -
(14,3 ± 15,2) mm
----------- Bei
einem senkrechten Wurf
nach oben tritt eine
West-Abweichung auf. Bei
Gleichheit von Steighöhe
des Wurfs und Fallhöhe
des freien Falls ist die
Westabweichung vierfach
(siehe Grammel).
-----------
Es bestätigt sich also das Zitat von Carl Friedrich Gauß: ...
das die Fallversuche
wenig geeignet sind
die Drehbewegungen
der Erde erkennbar
zu machen,
da sie nach den
kostspieligsten
Zurüstungen doch
immer nur höchst
rohe Resultate
geben können.
|
letzte Änderung: 3. Okt. 2022