Home:

Pysics and Astronomy


Catenary Applet

instructions
A catenary is the curve assumed by a hanging chain or cable under its own weight when supported only at its ends.

"The equation was obtained by Leibniz, Huygens, and Johann Bernoulli in 1691 in response to a challenge by Jakob Bernoulli." (Wolfram MathWorld)

catenary curve equation

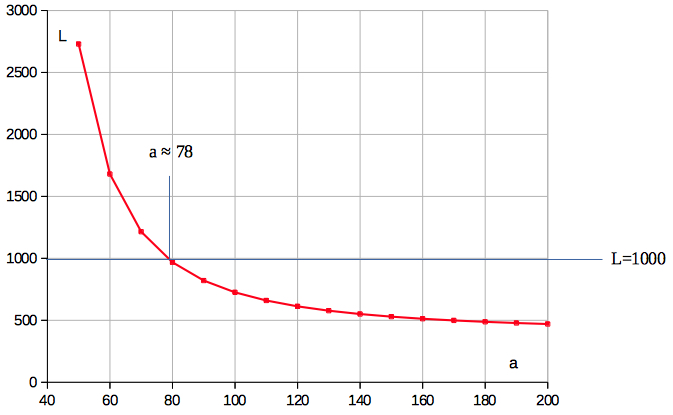
From length L of the chain and width W (distance of suspensions) the parameter a can be calculated by an iteration.
length
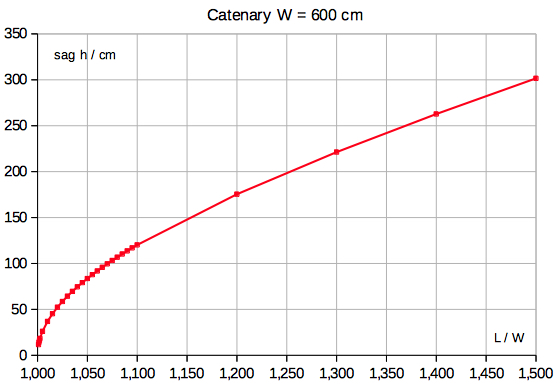
The catenary sag h is the vertical difference of the lowest point of the chain



abc
 Check a radio button to set the points A, B, or C (intermediate).
mass per length
 µ is the mass per length of the chain (kg / m).
length width
 Input for the ratio of length L and width AB (L>W).
input length width    
Having changed µ or L/W press button "Apply input".
step
 Step to change the ratio L/W.
increase decrease
plus key   minus key
 Use the buttons (+) or (-) to apply the selected step ∆(L/W) to increase or decrease the ratio L/W,
or use the keys.
curvature
 The radius r of curvature at the lowest point of the chain is r = a.


catenary sag

---

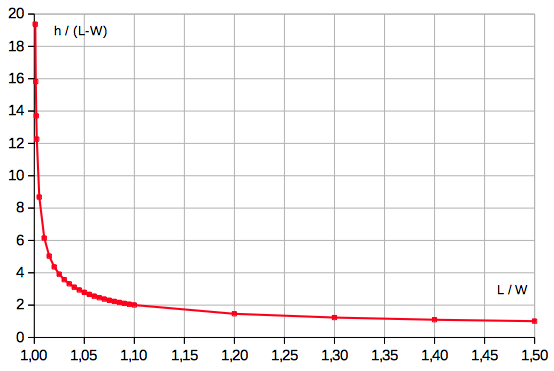
The curve below
h/(L-W) vs. L/W
does not depend on W:

Exemples:

for W=400 and L/W=1,2 (L=480, L-W=80, a=187.817):
h=116.9 and h/(L-W)=1.46

for W=600 and L/W=1,2 (L=720, L-W=120, a=281.725):
h=175.4 and h/(L-W)=1.46

for W=800 and L/W=1,2 (L=960, L-W=160, a=375.633):
h=233.9 and h/(L-W)=1.46

sag of catenary

---

A simple iteration:

iteration

length

double solveA(double L, double W)
{       
        double x, y;
        double A=0;

        for (int a=0; a<=50000; a++) {
            x = a;
            y = 2.0*x*Math.sinh(0.5*W/x);
            if (y<L) {
                A=x-1.0;
                break;
            }
        }
       
        for (int a=0; a<=12; a++) {
            x = A + 0.1*a;
            y = 2.0*x*Math.sinh(0.5*W/x);
            if (y<L) {
                A=x-0.1;
                break;
            }
        }

// repeat the steps to the desired precision

        return A;
}

Using series expansions for cosh(x) and sinh(x) in the equations y(x,a) and L(a,W) we get the approximations:

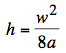approximation drag

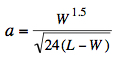approximation a

and, eliminating the parameter a:

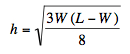
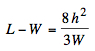approximation       approximation



Web Links
Catenary (Wikipedia)

Catenary (Wolfram MathWorld)

The Catenary (J. B. Calvert)

Cable’s Sag & Tension Calculation

Tension on the ends of a cable suspended at different heights

Microsoft Word - educated-monkey.doc


2017-2023  J. Giesen

updated: 2023, Oct 12

s