Hollow Earth Applet - Circle Inversion

Home

Site Map

GeoAstro
Applets

Astronomy

Chaos Game

Java

Miscel-
laneous

Hollow Earth Applet

Transformation by Circle Inversion

There are some people believing that we live in the interior of a hollow earth and that the universe itself lies within ("concave hollow-Earth hypothesis"). Cyrus Reed Teed proposed this idea in 1869.
There is indeed a coordinate transformation such that the interior of the Earth becomes "exterior" and the exterior becomes "interior": the transformation by circle inversion.

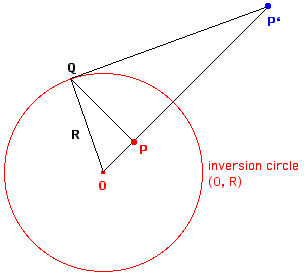
circle inversion
transformation

P' is the inverse of P with respect to the inversion circle, center O, radius R.

OP * OP' = R²

which follows from similar triangles: OP : R = R : OP'

Using rectangular coordinates formulae of the transformation from P(x,y) to P'(x',y') are:

circle inversion
transformation fomula

> name="Hollow Earth"

Instructions for use:

	To change the center of the inversion circle check the box "Earth Center" and click.
	Check the box "Earth Radius" and click to set the radius of the inversion circle.
	Check the boxes then draw a single point (A), or a line (AB), or a triangle (ABC) by clicking.
	Check the box to see the lines connecting the points.
	To draw a circle check the box "Circle Center" and click, then check "Circle Radius" and click to change the radius.
	Select items from the "Details" menu.
	Two points (A, B) or a circle selected will enable the "Motion Options" menu. Choose "Run" to start the animation. The uniform speed along the original straight line AB and along the circle is set to unity.

Some examples:

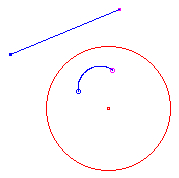line > arc of a circle	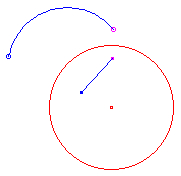arc of a circle > line
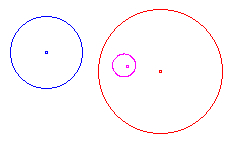circle <> circle
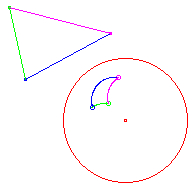triangle	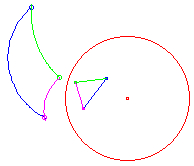triangle
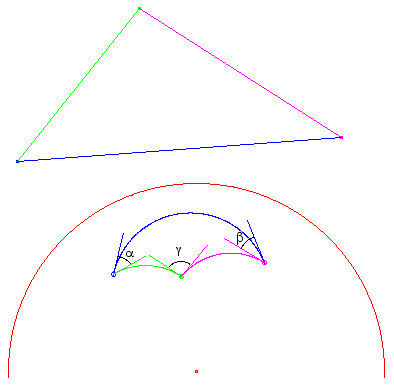The transformation is angle preserving. Select the item "Triangle Angles" from the "Details" menu. The angle sum (α+β+γ) of the transformed triangle is also 180°:
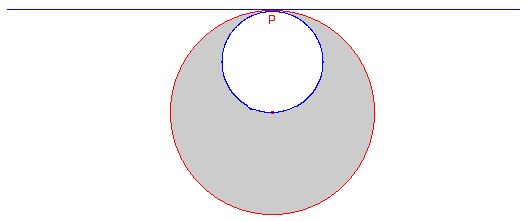The visible region of an observer at P is the white circle, the circumference (horizon) passing the center of the "hollow Earth".
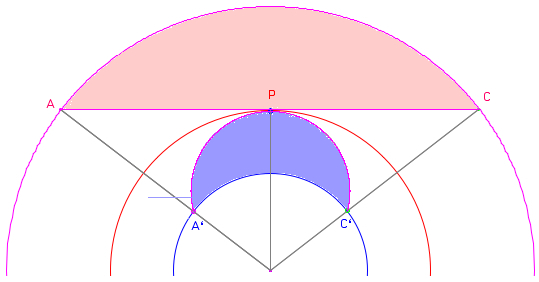The pink region of a geocentric sphere, as seen by an observer P, is transformed to the blue region inside the Earth.
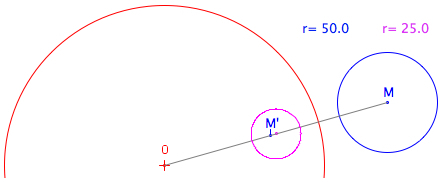The ratio of the radii r/r is equal to the ratio OM/OM'. (The image point M' of M is not the center of the image circle!)
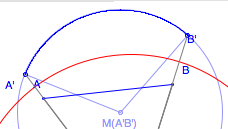If AB is inside the Earth, the length of the arc A'B' is greater than the length of the straight line AB.
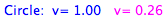	The ratio of the velocities of the moving points is inverse to the ratio of their distances from the center O.