Home Site Map Search

GeoAstro Applets

Astronomy

Chaos Game

Java

Miscel- laneous

Physics Quiz

Who is Who ?

Lines of Daylight Hours Sundial

	Enter latitude in decimal degrees and press return key,   enter longitude in decimal degrees and press return key.
Key commands:	you may use the keys "h", "d", "m", "n" to increase the hour, date, month, or minute, or Shift key and "h", "d", "m",  "n" to decrease the hour, date, month, or minute ! Click the applet first !
	Hold down the Control key and click into the applet area to shift the drawing. Use the "Details" options "Zoom in" or "Zoom out" for scaling.

The gnomon (length L) of this sundial is vertical. The shadow of it's top on the horizontal plane is used to read the sundial. The declination lines (gray) are computed for full numbers of daylight hours which depend on the latitude of the observer and the declination of the Sun (hour angle H): cos(H) = - tan(latitude)*tan(declination) H*15° is half of the diurnal arc of the Sun on the celestial sphere (from the local meridian to the horizon). Example: latitude 52.52° N, hour angle H=75° means 2*75/15 = 10 hours of daylight By the formula we get the declination -11.23° (occuring on Feb  18 and Oct  22) Select "Data Window" from the "Details" menu: For dec1=+23.44° and dec2=-23.44° we get the maximum and minimum of daylight: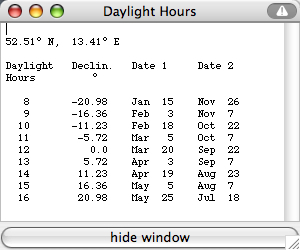 H1 = 124.4° or 2*124.4/15 = 16.6 hours of daylight (summer solstice) H2 = 55.6° or 2*55.6/15 = 7.4 hours of daylight (winter solstice) Connecting adjacent intersection points we get the lines of Italian hours (green lines). 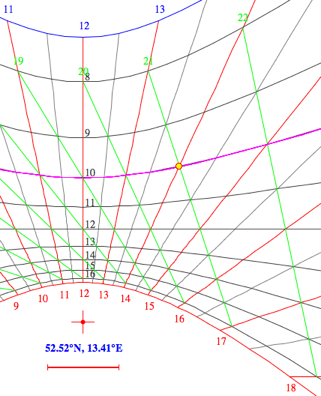Select "Italian Hours on/off" from the "Details" menu: Italian hours begin counting at sunset and end 24 hours later with the following sunset. Example: Standard Time 14:21 on Feb 19 (14:01 local time) is 3 hours before sunset (at 17:21 Standard Time), i.e. 21:00 in Italian hours, 3 hours before sunset. In this applet the times of sunrise and sunset are for h=0° altitude (discarding atmospheric refraction) instead of -0.83°. For low and mid latitudes the difference is only a few minutes. sin h = sin(lat) sin(dec) + cos(lat) cos(dec) cos(H) Setting the altitude to h=0: H = arc cos[-tan(lat) tan(dec)]

Updated: 2010, Feb 18

© 2010 J. Giesen